Дві бригади мали прокласти по 40 м кабелю. Одна з них щогодини прокладала на 2 метри більше за другу і закінчила на 1 годину раніше від неї. Скільки метрів кабелю прокладала щогодини кожна бригада?
Пусть х км/ч - собственная скорость лодки, тогда (х + 3) км/ч - скорость лодки по течению реки, (х - 3) км/ч - скорость лодки против течения реки. На путь туда и обратно затрачено 9 часов. Уравнение:
(см. объяснение)
Объяснение:
Введем функцию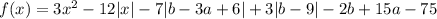 .
.
Заметим, что перед нами уравнение двух парабол, склеивающихся в фиксированной точке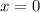 .
.
Этот график может ездить только вверх-вниз в зависимости от значений параметров и
и 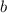 .
.
Уравнение может иметь ровно два корня при любом значении параметра
может иметь ровно два корня при любом значении параметра 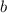 только, если
только, если 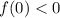 .
.
Тогда перейдем к неравенству:
Построим его в координатах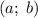 .
.
(см. прикрепленный файл)
Получили, что при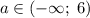 исходное уравнение имеет ровно два различных корня при любом значении параметра
исходное уравнение имеет ровно два различных корня при любом значении параметра 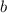 .
.
ответим теперь на вопрос задачи: ниже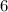 .
.
Задание выполнено!
Пусть х км/ч - собственная скорость лодки, тогда (х + 3) км/ч - скорость лодки по течению реки, (х - 3) км/ч - скорость лодки против течения реки. На путь туда и обратно затрачено 9 часов. Уравнение:
36/(х+3) + 36/(х-3) = 9
36 · (х - 3) + 36 (х + 3) = 9 · (х - 3) · (х + 3)
36х - 108 + 36х + 108 = 9 · (х² - 3²)
36х + 36х = 9х² - 81
72х = 9х² - 81
9х² - 72х - 81 = 0
Разделим обе части уравнения на 9
х² - 8х - 9 = 0
D = b² - 4ac = (-8)² - 4 · 1 · (-9) = 64 + 36 = 100
√D = √100 = 10
х₁ = (8-10)/(2·1) = (-2)/2 = -1 (не подходит, так как < 0)
х₂ = (8+10)/(2·1) = 18/2 = 9
ответ: 9 км/ч - собственная скорость лодки.
Проверка:
36 : (9 + 3) = 36 : 12 = 3 ч - по течению
36 : (9 - 3) = 36 : 6 = 6 ч - против течения
3 ч + 6 ч = 9 ч - туда и обратно