Два автомобиля выезжают одновременно из одного города в другой. Скорость первого на 20 км/ч больше скорости второго, поэтому первый автомобиль приезжает на место на 1/4 часа раньше второго. Найдите скорость каждого автомобиля, зная, что расстояние между городами равно 150 км.
Пусть скорость пешехода равна х км/ч, а велосипедиста - у км/ч. Пешеход и велосипедист встретились через 2 часа после выезда, поэтому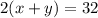 . После встречи пешеход прибыл в пункт Б на 5 ч20 мин позже, чем велосипедист в пункт А, поэтому
. После встречи пешеход прибыл в пункт Б на 5 ч20 мин позже, чем велосипедист в пункт А, поэтому 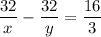
5ч 20мин = 5 + (20/20) = 5 + (1/3) = 16/3
Составим и решим систему уравнений
Умножим левую и правую части уравнения на 3y(16-y)/16≠0, имеем
По теореме Виета
Скорость пешехода равна 16 - 12 = 4 км/ч.
ответ: скорость пешехода - 4 км/ч и скорость велосипедиста - 12 км/ч
1)√28-√4*18-√4*12/√36*32+√16*48-√64*7=√28-√72-√48/√1152+√768-√448=-√92/√1472=
-√1/16=-1/4
ответ:-1/4
2)а)(√32-√9*12)*(√4*8+√108)
Сначала выполняем действие в первой скобочке:
√32-√108
Во второй скобочке:
√32+√108
У нас получается:(√32-√108)(√32+√108) =>формула сокращенного умножения=
(√32)^2+√108*√32-√108*√32-(√108)^2=32+√3456-√3456-108
√3456 сокращаются,и остается 32-108=-76
ответ:-76
б)(√4-√7)(√4+√7)=(√4)^2-√7*√4-√4*√7-(√7)^2=4+√28-√28-7=4+√28-√28-7
√28 сокращаются,и остается 4-7=-3
ответ:-3