Два насоси наповнюють басейн за 6 годин. За скільки годин міг би наповнити басейн кожен насос, працюючи окремо, якщо перший може це зробити на 5 годин швижше, ніж другий
Объяснение: Для начала построим график функции y = x² + x - 2
ординаты вершины: ,
Координаты точек пересечения с осями координат:
1) с ОХ: у = 0. x² + x - 2 = 0. По теореме Виета х₁ = 1, х₂ = -2. (1; 0), (-2; 0)
2) с ОУ: х = 0. у(0) = 0 + 0 - 2 = -2. (0; -2).
График - во вложении 1.
Из графика y = x² + x - 2 можно получить график функции y = |x² + x - 2|, если ту часть графика, которая ниже оси ОХ, "отзеркалить" относительно оси ОХ. В итоге получим график во вложении 2.
Прямая, параллельная оси абсцисс, имеет вид y = a, где а - произвольное число. Будем подбирать разные значения параметра а и посмотрим, какое максимальное кол-во общих точек будут иметь наша функция и прямая y = a. (вложение 3)
Если а < 0 (наглядный пример - а = -0,4), то общих точек не будет вообще.
Если а = 0 (прямая совпадает с осью ОХ), то имеем ровно две точки пересечения.
Если а = 9/4 (отзеркаленная вершина), то иметь будем 3 точки пересечения. А если брать промежуточные значения - 0 < a < 9/4 (наглядный пример - а = 1,5), - то будет 4 точки пересечения, т.е. 4 общих точки.
Если брать значения а > 9/4 (наглядный пример - а = 3), то у нас будет только 2 общих точки.
Итого: наибольшее число общих точек графиков наших функций - 4.
Y=x^2*(3-x) то есть корни х=0 и х=3 возьмем производную она равна 6х-3x^2=3x(2-x) точки экстремума х=0 и х=2 методом интервалов находим участки, где производная больше 0 (ф-я возрастает) и меньше 0 (ф-я убывает). Производная больше 0 при х∈(0;2) и отрицательна при х∈(-∞, 0)∨(2,∞). в точке х=2 максимум - производная меняет знак с + на -, а точка х=0 локальный минимум,точка перегиба, так как вторая производная равна 6-6х, есть 6-6х=0 или х=1. итак линия графика такая - она идет сверху вправо вниз до точки х=0, выпуклостью вниз, касается оси Х в точке х=0 и далее в точке х=1 выпуклостью вверх возрастает до точки х=2 и, затем, идет вниз, пересекая ось в точке х=3
ответ: 4.
Объяснение: Для начала построим график функции y = x² + x - 2
ординаты вершины: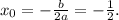 ,
, 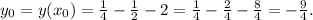
Координаты точек пересечения с осями координат:
1) с ОХ: у = 0. x² + x - 2 = 0. По теореме Виета х₁ = 1, х₂ = -2. (1; 0), (-2; 0)
2) с ОУ: х = 0. у(0) = 0 + 0 - 2 = -2. (0; -2).
График - во вложении 1.
Из графика y = x² + x - 2 можно получить график функции y = |x² + x - 2|, если ту часть графика, которая ниже оси ОХ, "отзеркалить" относительно оси ОХ. В итоге получим график во вложении 2.
Прямая, параллельная оси абсцисс, имеет вид y = a, где а - произвольное число. Будем подбирать разные значения параметра а и посмотрим, какое максимальное кол-во общих точек будут иметь наша функция и прямая y = a. (вложение 3)
Если а < 0 (наглядный пример - а = -0,4), то общих точек не будет вообще.
Если а = 0 (прямая совпадает с осью ОХ), то имеем ровно две точки пересечения.
Если а = 9/4 (отзеркаленная вершина), то иметь будем 3 точки пересечения. А если брать промежуточные значения - 0 < a < 9/4 (наглядный пример - а = 1,5), - то будет 4 точки пересечения, т.е. 4 общих точки.
Если брать значения а > 9/4 (наглядный пример - а = 3), то у нас будет только 2 общих точки.
Итого: наибольшее число общих точек графиков наших функций - 4.
возьмем производную она равна 6х-3x^2=3x(2-x)
точки экстремума х=0 и х=2
методом интервалов находим участки, где производная больше 0 (ф-я возрастает) и меньше 0 (ф-я убывает). Производная больше 0 при х∈(0;2) и отрицательна
при х∈(-∞, 0)∨(2,∞). в точке х=2 максимум - производная меняет знак с + на -, а точка х=0 локальный минимум,точка перегиба, так как вторая производная равна 6-6х, есть 6-6х=0 или х=1.
итак линия графика такая - она идет сверху вправо вниз до точки х=0, выпуклостью вниз, касается оси Х в точке х=0 и далее в точке х=1 выпуклостью вверх возрастает до точки х=2 и, затем, идет вниз, пересекая ось в точке х=3