Два стеклянных и девятнадцать оловянных шариков разделили на три кучки по 7 шариков. Какова вероятность того, что стеклянные шарики окажутся в разных кучках?
Переведем минуты в часы: 6 минут=6/60 часа= 1/10=0.1 часа.
Пусть второй рабочий обрабатывает 1 деталь за х часов, тогда первый - за (х+0.1) часа. За 7 часов работы второй обработает деталей, а первый за 7 часов обработает деталей.
7 (х+0.1)-7х=8*х*(х+0.1)
0.7=8+0.8х
D=
x1,2=(-0,8±4.8)/16
x=0,25 = часа = 15 минут обрабатывает второй рабочий 1 деталь
а первый на 6 минут дольше, т.е. 15+6=21 минуту или 0.25+0.1=0.35 часа
Первый за 7 часов обрабатывает 7: 0.35=20 деталей,
Первый рабочий - 20 деталей, второй - 28 деталей
Объяснение:
Переведем минуты в часы: 6 минут=6/60 часа= 1/10=0.1 часа.
Пусть второй рабочий обрабатывает 1 деталь за х часов, тогда первый - за (х+0.1) часа. За 7 часов работы второй обработает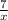
деталей, а первый за 7 часов обработает 
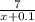деталей.
7 (х+0.1)-7х=8*х*(х+0.1)
0.7=8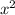
+0.8х
D=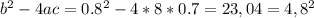
x1,2=(-0,8±4.8)/16
x=0,25 =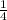
часа = 15 минут обрабатывает второй рабочий 1 деталь
а первый на 6 минут дольше, т.е. 15+6=21 минуту или 0.25+0.1=0.35 часа
Первый за 7 часов обрабатывает 7: 0.35=20 деталей,
а второй 7:0,25= 28 деталей
x принадлежит [-1,1]
Объяснение:
-x^2+4-3>=0
-x^2+1>=0
Перенесём постоянную в правую часть и сменим её знак:
-x^2+1-1>=0-1
Сократим противоположные выражения:
-x^2>0-1
-x^2>=-1
Сменим знаки обеих частей неравенства и поменяем знак неравенства на противоположный:
-1x*(-x^2)<=-1x*(-1)
x^2<=-1*(-1)
x^2<=1
Извлечём √ из обеих частей неравенства:
√x^2<=√1
Сократим степень корня и показатель степени на 2:
(x)<=√1
Разделим неравенство на 2 возможных случая :
x<=1,x<=0
-x<=1,x<0
Найдём пересечение :
x принадлежит [0,1]
-x<=1,x<0
Решим уравнение относительно х:
-x<=1
Умножим обе части неравенства на -1 и перевернём знак неравенства :
-1*(-x)>=-1*1
x>=-1*1
x>=-1
Найдём пересечение : x принадлежит [0,1]
x принадлежит [-1,0]
Найдём объединение :
x принадлежит [-1,1]
x принадлежит [-1,1]