Екі параллель түзуді қиюшымен қиғанда шыққан бұрыштардың бірі 77°. Қалған бұрыштарды табыңыз.

Показать ответ

Ответ:

narek2006

25.09.2020 13:41

ответ:Составим систему уравнений, приняв каждое из чисел, равным Х и У. При этом, если остаток от деления чисел равен 4-м, а неполное частное - 3-м, значит одно из чисел, уменьшенное на 4, будет делиться на второе число без остатка и будет равно 3-м. Среднее арифметическое двух чисел равно сумме этих чисел, деленных на 2:

(Х – 4) / У = 3;

(Х + У) / 2 = 18

Х + У = 2 * 18;

Х + У = 36;

Х = 36 – У;

(Х – 4) / У = 3;

(36 – У – 4) / У = 3;

(32 - У) / У = 3;

32 – У = 3 * У;

32 = 3 * У + У = 4 * У;

У = 32 / 4 = 8;

Х = 36 – У = 36 – 8 = 28.

Проверим:

(8 + 28) / 2 = 36/2 = 18;

28/8 = (24 + 4) / 8 = 24/8 + 4/8 = 3 + 4/8 = 3 (ост. 4).

Объяснение:

0,0(0 оценок)

Ответ:

leonidbobnev

04.10.2021 20:45

Смотри решение.

Объяснение:

решения (через дискриминант):

$x^2+5x+6=0\\a=1; b=5; c=6\\D=b^2-4ac\\D=5^2-4*1*6\\D=25-24\\D=1\\\sqrt{D}=\sqrt{1}=1\\x_{1}=\frac{-b+\sqrt{D}}{2a}=\frac{-5+1}{2}=\frac{-4}{2}=-\frac{4}{2}=-2\\x_{2}=\frac{-b-\sqrt{D}}{2a}=\frac{-5-1}{2}=\frac{-6}{2}=-\frac{6}{2}=-3\\$

Порядок решения:

а. Записываем уравнение в исходном виде;

б. Находим дискриминант (дискриминант должен получиться больше 0 (2 корня уравнения), или равным 0 (1 корень уравнения), если дискриминант меньше 0, то уравнение не имеет корней, и дальше его нет смысла решать);

в. Находим корни уравнения, при условии того, что написано в предыдущем пункте.

решения (через теорему Виетта):

Сумма 2 корней уравнения равняется коэффициенту b, взятому с противоположным знаком.

Произведение 2 корней уравнения равняется свободному коэффициенту в данном уравнении.

Общая формула квадратного уравнения: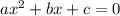 $ax^2+bx+c=0\\$ (для справок).