Экзамену по математике должна предшествовать консультация, причем консультация не проводится в день экзамена. Сессия длится 6 дней: с понедельника по субботу. В каждый из этих дней преподаватель успевает провести только три занятия.
У скольких групп успеет принять экзамен преподаватель за сессию, если:
а) для каждой группы проводится отдельная консультация
б) консультации отдельных групп можно объединять, но не более чем у трех групп
в) консультации отдельных групп можно объединять
1. x^2 + 2x + a = 0
2. D = 2^2 - 4 * 1a
3. D = 4 - 4a
4. (4 - 4a > 0
(4 - 4a = 0
(4 - 4a < 0
5. (a < 1
(a = 1
(a > 1
6. (a < 1 , 2 действительных корня.
(a = 1 , 1 действительный корень.
(a > 1 , нет действительных корней.
Объяснение:
1. Определим количество корней с дискриминанта: D = b^2 - 4ac.
2. Упростим выражение.
3. Есть три возможных случая: D > 0, D = 0, D < 0.
4.1 Решим неравенство относительно a.
4.2 Решим уравнение относительно a.
4.3 Решим неравенство относительно a.
5. Когда D > 0, есть 2 действительных корня, когда D = 0, есть 1 действительный корень, когда D < 0, нет действительных корней.
1. Уравнение можно решить так же, как это сделал(а) Agnesmile02464, но можно ещё сделать через дискриминант.
x^2 - 6x - 7 = 0
D = b^2 - 4ac;
D = -6^2 - 4 * 1 * (-7) = 36 + 28 = 64
x = (-b +-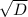
)/2a
x1 = (6 +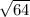
)/2 * 1 = (6 + 8)/2 = 14/2 = 7
x2 = (6 -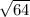
)/2 * 1 = (6 - 8)/2 = -2/2 = -1
2. Для решения этого задания есть специальная формула, но я её благополучно забыл.) Попробую решить через систему. Для решения этого задания нам понадобится всеми любимая формула y=kx + b. Нужно взять две любые точки, через которые проходит прямая, и подставить. Получаем:
(-1;3) и (1;-3)
Подставляем в формулу, получаем систему:
{3 = -k + b
{-3 = k + b
Перенесем значения, чтобы были легче:
{k - b = -3
{-k - b = 3
Нам нужно найти k и b. Отнимем эти уравнения, чтобы избавиться от b и, для начала, найти k:
k - b - (-k) - (-b) = -3 - 3
k - b + k + b = -6
2k = -6
k = -3
Подставим в саааамое первое уравнение:
3 = - (-3) + b
3 = 3 + b
-b = 3 - 3
b = 0
k = -3, b = 0. Подставляем значения в y = kx + b и получаем функцию:
y = -3x
ответ 1)
Объяснение: Если что-то непонятно - не стесняйся и спрашивай ;)