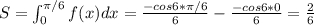площадь можно найти с интеграла. для начала находим первообразную функции
F(x)=-cos6x/6+C
теперь S=\int_{0}^{\pi /6}f(x)dx=\frac{-cos6*\pi /6}{6}-\frac{{-cos6*0}}{6}=\frac{2}{6}
площадь можно найти с интеграла. для начала находим первообразную функции
F(x)=-cos6x/6+C
теперь S=\int_{0}^{\pi /6}f(x)dx=\frac{-cos6*\pi /6}{6}-\frac{{-cos6*0}}{6}=\frac{2}{6}