ответ max ab=25
Решение задачи прилагаю
25
Объяснение:
1-ый
Произведение ab будет наибольшим тогда, когда a=b.
Опираясь на это утверждение, получим уравнение:
Подставим найденное значение в произведение:
2-ой
Теперь очевидно, что наибольшее значение ab достигается при и .
Найдем это значение при :
Тогда наибольшее значение ab - это 25.
Задание выполнено!
ответ max ab=25
Решение задачи прилагаю
25
Объяснение:
1-ый
Произведение ab будет наибольшим тогда, когда a=b.
Опираясь на это утверждение, получим уравнение:
Подставим найденное значение в произведение:
2-ой
Теперь очевидно, что наибольшее значение ab достигается при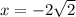 и
и 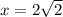 .
.
Найдем это значение при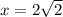 :
:
Тогда наибольшее значение ab - это 25.
Задание выполнено!