Данное двойное неравенство равносильно системе двух квадратных неравенств:
Первое неравенство .
Заметим, что в левой части скрывается квадрат разности (формула ): .
Неравенство принимает следующий вид: .
Так как квадрат числа всегда неотрицательный, то нам не подходит всего лишь один случай: и .
Значит, первой неравенство эквивалентно тому, что .
Второе неравенство .
Вс уравнение имеет по теореме Виета (утверждающей, что и ) корни и .
Из этого следует разложение левой части на множители: .
Метод интервалов подсказывает решение .
+ + + - - - + + +
___________________________
\\\\\\\\\\\\\\\\\\\\\
Значит, второе неравенство равносильно тому, что .
Имеем значительно более простую систему неравенств:
Вполне понятно, что ее решением является (как пересечения двух промежутков).
Или же .
Задача решена!
Объяснение:
1) Общий член арифметической прогрессии an = a1 + d (n - 1).
a1 = - 14;
a2 = -11 = - 14 + d;
d = 3;
a23 = - 14 + 3 * 22 = 52.
Найдём сумму первых 23 членов этой арифметической прогрессии:
S23 = 23 (a1 + a23) / 2 = 23 * 19 = 437.
2) Найдём одиннадцатый член этой арифметической прогрессии:
a1 = 17,2;
a11 = 17,2 - 0,2 * 10 = 15,2;
Сумма одиннадцати членов равна:
S11 = 11 * (17,2 + 15,2)/2 = 178,2.
3) Найдём двадцать второй член этой арифметической прогрессии:
a1 = 6;
a10 = 12,3 = 6 +9 d;
d = 0,7;
a20 = 6 + 0,7 * 19 = 19,3.
Найдём сумму 22 членов этой арифметической прогрессии:
S22 = 22 * (6 + 19,3)/2 = 278,3.
Данное двойное неравенство равносильно системе двух квадратных неравенств:
Первое неравенство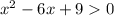 .
.
Заметим, что в левой части скрывается квадрат разности (формула ):
): 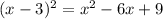 .
.
Неравенство принимает следующий вид: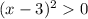 .
.
Так как квадрат числа всегда неотрицательный, то нам не подходит всего лишь один случай: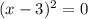 и
и 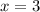 .
.
Значит, первой неравенство эквивалентно тому, что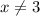 .
.
Второе неравенство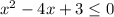 .
.
Вс уравнение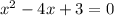 имеет по теореме Виета (утверждающей, что
имеет по теореме Виета (утверждающей, что 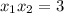 и
и 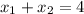 ) корни
) корни 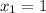 и
и 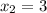 .
.
Из этого следует разложение левой части на множители: .
.
Метод интервалов подсказывает решение![x \in [ 1; 3 ]](/tpl/images/1227/3957/60bcc.png) .
.
+ + + - - - + + +
_________![[ \; 1 \; ]](/tpl/images/1227/3957/d73a9.png) _________
_________![[ \; 3 \; ]](/tpl/images/1227/3957/abab5.png) _________
_________
\\\\\\\\\\\\\\\\\\\\\
Значит, второе неравенство равносильно тому, что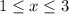 .
.
Имеем значительно более простую систему неравенств:
Вполне понятно, что ее решением является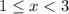 (как пересечения двух промежутков).
(как пересечения двух промежутков).
Или же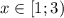 .
.
Задача решена!
ответ:Объяснение:
1) Общий член арифметической прогрессии an = a1 + d (n - 1).
a1 = - 14;
a2 = -11 = - 14 + d;
d = 3;
a23 = - 14 + 3 * 22 = 52.
Найдём сумму первых 23 членов этой арифметической прогрессии:
S23 = 23 (a1 + a23) / 2 = 23 * 19 = 437.
2) Найдём одиннадцатый член этой арифметической прогрессии:
a1 = 17,2;
a11 = 17,2 - 0,2 * 10 = 15,2;
Сумма одиннадцати членов равна:
S11 = 11 * (17,2 + 15,2)/2 = 178,2.
3) Найдём двадцать второй член этой арифметической прогрессии:
a1 = 6;
a10 = 12,3 = 6 +9 d;
d = 0,7;
a20 = 6 + 0,7 * 19 = 19,3.
Найдём сумму 22 членов этой арифметической прогрессии:
S22 = 22 * (6 + 19,3)/2 = 278,3.