Для выяснения сходимости ряда используем признак Лейбница.
Очевидно, что
1. , так как с увеличением номера n увеличивается знаменатель, а с ростом знаменателя дробь становится все меньше и меньше;
2.
Надеюсь, данный факт ясен.
Два условия выполнены, следовательно, ряд по признаку Лейбница сходится.
Выясним вопрос относительно абсолютной сходимости. Для этого нужно рассмотреть соответствующий ряд из модулей исходного ряда.
Напомню, что модуль "съедает" множитель вида . Значит, общий член нового ряда имеет вид .
Для установления сходимости данного ряда используем интегральный признак Коши. Это можно сделать, поскольку действительнозначная функция
неотрицательна, непрерывна и убывает на интервале
Можно рассмотреть несобственный интеграл. Исследуем его на сходимость. подробности в приложенном файле.
Итак, получена бесконечность, стало быть, несобственный интеграл расходится.
Ряд сходится либо расходится вместе с несобственным интегралом. То есть, расходится.
Таким образом, сам ряд сходится. Но ряд из модулей расходится, что исключает абсолютную сходимость ряда. А сходящийся ряд, не сходящийся абсолютно, сходится условно.
Тригонометрия – математическая дисциплина, изучающая зависимость между сторонами и углами треугольника, является разделом геометрии, тригонометрические функции являются объектом изучения математического анализа, а тригонометрические уравнения изучаются методами алгебры.
Тригонометрические функции возникли в Древней Греции в связи с исследованиями в астрономии и геометрии. Отношения сторон в прямоугольном треугольнике, которые по существу и являются тригонометрическими функциями, встречаются уже в Ш в. до н. э. в работах Евклида, Архимеда, Аполлония Пергского и др. Тригонометрия от греческих: trigonom – “треугольник”, metreo – “измеряю”, изучает зависимость между сторонами и углами треугольника.
Тригонометрия возникла из пратических нужд человека. С ее можно определить расстояния до недоступных предметов. Она существенно упрощает процесс геодезической съемки местности, нужный для составления карт.
Зачатки тригонометрических познаний родились в древности. Жрецы постоянно наблюдали за небом, за перемещением звезд. На раннем этапе тригонометрия развивалась в тесной связи с астрономией и являлась ее вс разделом.
Исторически теоремы синусов сферической геометрии предшествовали теоремам плоской геометрии. Потребность людей в знаниях по астрономии, необходимых для исчисления времени, возникла прежде других потребностей человека, связанных с измерением углов. Исходя из геоцентрической гипетезы Вселенной, древнегреческие астрономы рассматривали Землю как шар, находящийся в центре небесной сферы, которая рвномерно вращается вокруг своей оси. При изучении закономерностей движения светил возникли многочисленные математические задачи, связанные со свойствами сферы и фигур, которые образуют на ней большие окружности.
условно сходится
Объяснение:
Для выяснения сходимости ряда используем признак Лейбница.
Очевидно, что
1.
, так как с увеличением номера n увеличивается знаменатель, а с ростом знаменателя дробь становится все меньше и меньше;
2.
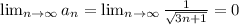
Надеюсь, данный факт ясен.
Два условия выполнены, следовательно, ряд по признаку Лейбница сходится.
Выясним вопрос относительно абсолютной сходимости. Для этого нужно рассмотреть соответствующий ряд из модулей исходного ряда.
Напомню, что модуль "съедает" множитель вида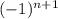
. Значит, общий член нового ряда имеет вид 
.
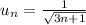Для установления сходимости данного ряда используем интегральный признак Коши. Это можно сделать, поскольку действительнозначная функция
неотрицательна, непрерывна и убывает на интервале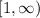
Можно рассмотреть несобственный интеграл. Исследуем его на сходимость. подробности в приложенном файле.
Итак, получена бесконечность, стало быть, несобственный интеграл расходится.
Ряд сходится либо расходится вместе с несобственным интегралом. То есть, расходится.
Таким образом, сам ряд сходится. Но ряд из модулей расходится, что исключает абсолютную сходимость ряда. А сходящийся ряд, не сходящийся абсолютно, сходится условно.
Тригонометрия – математическая дисциплина, изучающая зависимость между сторонами и углами треугольника, является разделом геометрии, тригонометрические функции являются объектом изучения математического анализа, а тригонометрические уравнения изучаются методами алгебры.
Тригонометрические функции возникли в Древней Греции в связи с исследованиями в астрономии и геометрии. Отношения сторон в прямоугольном треугольнике, которые по существу и являются тригонометрическими функциями, встречаются уже в Ш в. до н. э. в работах Евклида, Архимеда, Аполлония Пергского и др. Тригонометрия от греческих: trigonom – “треугольник”, metreo – “измеряю”, изучает зависимость между сторонами и углами треугольника.
Тригонометрия возникла из пратических нужд человека. С ее можно определить расстояния до недоступных предметов. Она существенно упрощает процесс геодезической съемки местности, нужный для составления карт.
Зачатки тригонометрических познаний родились в древности. Жрецы постоянно наблюдали за небом, за перемещением звезд. На раннем этапе тригонометрия развивалась в тесной связи с астрономией и являлась ее вс разделом.
Исторически теоремы синусов сферической геометрии предшествовали теоремам плоской геометрии. Потребность людей в знаниях по астрономии, необходимых для исчисления времени, возникла прежде других потребностей человека, связанных с измерением углов. Исходя из геоцентрической гипетезы Вселенной, древнегреческие астрономы рассматривали Землю как шар, находящийся в центре небесной сферы, которая рвномерно вращается вокруг своей оси. При изучении закономерностей движения светил возникли многочисленные математические задачи, связанные со свойствами сферы и фигур, которые образуют на ней большие окружности.