ответ: 1-б. 2-а, 3-г, 4-, 5- , 6-в, 7-г
Объяснение:
1. Найдите значение алгебраической дроби 2х/х-1, при х= 1/3
• а) 0,75; б) -0,75 ; в) - ;г) -1,5
2. Найдите значение x, при котором дробь х+2/х-4 не имеет смысла
а)4 б)-2 в) -4 г) нет таких значений
3. Какое из предложенных выражений записано в виде алгебраической дроби?
а)2х/3+х ; б)2/х2+3х в)81х2/13-х ; г)2/3-х
4. Найдите значение выражения , при а= -0,7, в=0,3
а)2,5; б) -2,5; в) 1; г) другой ответ.
5.При каком значении а дробь не определена?
а) 0; б) - ; в) ; г)другой ответ.
6. Найди допустимые значения букв, входящих в дробь а/b
а) любые значения; б)5 возможных значений ; в) любые значения а и b, при b не равным 0 ; г) нет ответа
7.Выберите дробно- рациональные выражения 2х/3+4/7, 2-5х/7,3, 3/х-2
а) нет правильного ответа ; б) 2х/3+4/7 ; в)2-5х/7,3 ; г) 3/х-2
1) (sin 54° - sin 36°) : sin 9° = 2 cos 0.5( 54° + 36°) · sin 0.5(54° - 36°) : sin 9° =
= 2cos 45° · sin 9° : sin 9° = 2 cos 45° = 2 · 0.5 √2 = √2
2) (cos 25° + cos 85°) : cos 55° =
= 2 cos 0.5(25° + 85°) · cos 0.5(25° - 85°) : cos 55° =
= 2 cos 55° · cos 30° : cos 55° = 2 cos 30° = 2 · 0.5 √3 = √3
3) (sin 16° + sin 74°) : (cos 16° + cos 74°) =
= 2 sin 0.5(16° + 74°) · cos 0.5(16° - 74°) : (2 cos 0.5(16° + 74°) ·
· cos 0.5(16° - 74°)) = 2 sin 45° · cos 29° : (2 cos 45° · cos 29°) =
= sin 45° : cos 45° = tg 45° = 1
4) (cos 12° - cos 78°) : (sin 12° - sin 78°) =
= - 2 sin 0.5( 12° + 78°) · sin 0.5( 12° - 78°) : (2 cos 0.5 (12° + 78°) ·
· sin 0.5( 12° - 78°) = 2 sin 45° · sin 33° : (2 cos 45° · (-sin 33°)) =
= sin 45° : (- cos 45°) = -tg 45° = -1
5) (cos 40° - cos 80°) : (1 - 2sin² 35°) = - 2 sin 0.5( 40° + 80°) ·
· sin 0.5( 40° - 80°) : cos 70° = 2 sin 60° · sin 20° : cos (90 ° - 20°) =
= 2 sin 60° · sin 20° : sin 20° = 2 sin 60° = 2 · 0.5 √3 = √3
6) (sin 37° - sin 53°) : (2cos² 36° - 1) = 2 cos 0.5 (37° + 53°) ·
· sin 0.5 (37° - 53°) : cos 72° = 2 cos 45° · (-sin 8°) : cos (90° - 8°) =
= -2 cos 45° · sin 8° : sin 8° = - 2 cos 45° = -2 · 0.5 √2 = -√2
ответ: 1-б. 2-а, 3-г, 4-, 5- , 6-в, 7-г
Объяснение:
1. Найдите значение алгебраической дроби 2х/х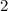
-1, при х= 1/3
• а) 0,75; б) -0,75 ; в) - ;г) -1,5
2. Найдите значение x, при котором дробь х+2/х-4 не имеет смысла
а)4 б)-2 в) -4 г) нет таких значений
3. Какое из предложенных выражений записано в виде алгебраической дроби?
а)2х/3+х ; б)2/х2+3х в)81х2/13-х ; г)2/3-х
4. Найдите значение выражения , при а= -0,7, в=0,3
а)2,5; б) -2,5; в) 1; г) другой ответ.
5.При каком значении а дробь не определена?
а) 0; б) - ; в) ; г)другой ответ.
6. Найди допустимые значения букв, входящих в дробь а/b
а) любые значения; б)5 возможных значений ; в) любые значения а и b, при b не равным 0 ; г) нет ответа
7.Выберите дробно- рациональные выражения 2х/3+4/7, 2-5х/7,3, 3/х-2
а) нет правильного ответа ; б) 2х/3+4/7 ; в)2-5х/7,3 ; г) 3/х-2
1) (sin 54° - sin 36°) : sin 9° = 2 cos 0.5( 54° + 36°) · sin 0.5(54° - 36°) : sin 9° =
= 2cos 45° · sin 9° : sin 9° = 2 cos 45° = 2 · 0.5 √2 = √2
2) (cos 25° + cos 85°) : cos 55° =
= 2 cos 0.5(25° + 85°) · cos 0.5(25° - 85°) : cos 55° =
= 2 cos 55° · cos 30° : cos 55° = 2 cos 30° = 2 · 0.5 √3 = √3
3) (sin 16° + sin 74°) : (cos 16° + cos 74°) =
= 2 sin 0.5(16° + 74°) · cos 0.5(16° - 74°) : (2 cos 0.5(16° + 74°) ·
· cos 0.5(16° - 74°)) = 2 sin 45° · cos 29° : (2 cos 45° · cos 29°) =
= sin 45° : cos 45° = tg 45° = 1
4) (cos 12° - cos 78°) : (sin 12° - sin 78°) =
= - 2 sin 0.5( 12° + 78°) · sin 0.5( 12° - 78°) : (2 cos 0.5 (12° + 78°) ·
· sin 0.5( 12° - 78°) = 2 sin 45° · sin 33° : (2 cos 45° · (-sin 33°)) =
= sin 45° : (- cos 45°) = -tg 45° = -1
5) (cos 40° - cos 80°) : (1 - 2sin² 35°) = - 2 sin 0.5( 40° + 80°) ·
· sin 0.5( 40° - 80°) : cos 70° = 2 sin 60° · sin 20° : cos (90 ° - 20°) =
= 2 sin 60° · sin 20° : sin 20° = 2 sin 60° = 2 · 0.5 √3 = √3
6) (sin 37° - sin 53°) : (2cos² 36° - 1) = 2 cos 0.5 (37° + 53°) ·
· sin 0.5 (37° - 53°) : cos 72° = 2 cos 45° · (-sin 8°) : cos (90° - 8°) =
= -2 cos 45° · sin 8° : sin 8° = - 2 cos 45° = -2 · 0.5 √2 = -√2