Касание — значит, одна точка пересечения. Тогда система уравнений, составленная из уравнений окружности и прямой, должна иметь одно решение:
Система имеет два решения, одно из них равно нулю. Чтобы решение было единственным, нужно, чтобы второй корень так же равнялся нулю. Тогда корни совпадут.
-1,5
Объяснение:
Такая окружность задаётся уравнением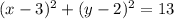
Касание — значит, одна точка пересечения. Тогда система уравнений, составленная из уравнений окружности и прямой, должна иметь одно решение:
Система имеет два решения, одно из них равно нулю. Чтобы решение было единственным, нужно, чтобы второй корень так же равнялся нулю. Тогда корни совпадут.