Найдём функцию Эйлера от числа 15. Это количество чисел, меньших 15 и взаимно простых с ним, то есть не имеющих с 15 общих делителей. Такими числами являются 1, 2, 4, 7, 8, 11, 13, 14, поскольку они не делятся ни на 3, ни на 5. Тогда функция Эйлера φ(15) = 8.
Так как 2 и 15 — взаимно простые числа, то сравнимо с 1 по модулю 15.
Тогда можно записать в виде
Поскольку мы выяснили, что сравнимо с 1 по модулю 15, то также сравнимо с 1 по модулю 15.
Остаётся , которое сравнимо с 8 по модулю 15, поскольку даёт остаток 8 при делении на 15.
Объяснение:
√81*0,25=√9*9*0,5*0,5=9*0,5=4,5.
√14,4*3,6=√ 14,4*10/10*3,6*10/10=√144*36*100/100=12*6/10=7,2.
√64*0,04=√8*8* 0,2*0,2=8*0,2=1,6.
√4/25=√2*2/5*5=2/5=0,4.
√7 1/9=√64/9=√8*8/3*3=8/3=2 2/3.
√1 11/25=√36/25=6/5=1 1/5.
√72*32=√8*9*8*2*2=8*3*2=48.
√0,64*9=0,8*3=2,4.
√4,9*12,1=√4,9*10*12,1*10/100=√7*7*11*11/100=7*11/10=7,7.
√3,6*250=√36*25=6*5=30.
√25/16=5/4=1 1/4=1.25.
√1 19/81=√100/81=10/9=1 1/9.
√3 6/25=√81/25=9/5=1 4/5=1,8.
√98*18=√2*7*7*2*3*3=2*7*3=42.
√9*36=3*6=18.
√0,49*25=0,7*5=3,5.
√100*0,64=10*0,8=8.
√4/9=2/3.
√81/100=9/10.
√169/225=13/15.
√810*40=√810/10*40*10=√81*400=9*20=180.
8
Объяснение:
Найдём функцию Эйлера от числа 15. Это количество чисел, меньших 15 и взаимно простых с ним, то есть не имеющих с 15 общих делителей. Такими числами являются 1, 2, 4, 7, 8, 11, 13, 14, поскольку они не делятся ни на 3, ни на 5. Тогда функция Эйлера φ(15) = 8.
Так как 2 и 15 — взаимно простые числа, то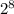 сравнимо с 1 по модулю 15.
сравнимо с 1 по модулю 15.
Тогда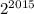 можно записать в виде
можно записать в виде 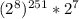
Поскольку мы выяснили, что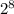 сравнимо с 1 по модулю 15, то
сравнимо с 1 по модулю 15, то 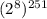 также сравнимо с 1 по модулю 15.
также сравнимо с 1 по модулю 15.
Остаётся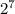 , которое сравнимо с 8 по модулю 15, поскольку даёт остаток 8 при делении на 15.
, которое сравнимо с 8 по модулю 15, поскольку даёт остаток 8 при делении на 15.
То есть можем записать: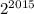 ≡
≡ 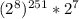 ≡
≡ 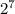 ≡ 8 mod 15
≡ 8 mod 15
Это значит, что остаток равен 8.