Проводя различные измерения, решая уравнения графическим выполняя арифметические вычисления, часто получают приближенные значения, а не точные. Например, при вычислении корня числа может получиться бесконечная непериодическая дробь (т. е. иррациональное число). Кроме того, существуют бесконечные периодические дроби, использовать которые в вычислениях также неудобно.
Поэтому числа, являющиеся бесконечными десятичными дробями или конечными, но имеющими множество знаков после запятой, принято округлять.
Когда округление выполняется в большую сторону, то говорят о приближении по избытку. Когда округление выполняется в меньшую сторону, то говорят о приближении по недостатку.
Полученное при округлении число называют приближенным по недостатку или избытку с определенной точностью. Рассмотрим несколько примеров приближения.
Число π является бесконечной дробью 3,1415926535... Обычно его округляют с точностью до 0,01. Это значит, что после запятой оставляют только два знака. При приближении по избытку получится 3,15. При приближении по недостатку получится 3,14.
Для числа π обычно используют приближение по недостатку, так как согласно правилу округления положительные числа округляются в большую сторону, если первая отбрасываемая цифра 5 или больше пяти. Так как у числа π третья цифра после запятой — это 1, то округление выполняется в меньшую сторону, то есть для расчетов выполняется приближение по недостатку.
Однако, несмотря на правила округления, имеют право быть приближения как по недостатку, так и по избытку.
Если выполнять приближение числа π с точностью до 0,0001, то по избытку получим π ≈ 3,1416, а по недостатку π ≈ 3,1415.
Рассмотрим иррациональное число √2, которое равно 1,414213... . Вычислим его приближение по недостатку и по избытку с точностью до 0,001. Поскольку приближение выполняется до тысячных долей, то у числа надо оставить три знака после запятой. При приближении по недостатку просто отбрасываются все цифры после третьей после запятой. При приближении по избытку цифры после третьей после запятой отбрасываются, а третья цифра увеличивается на 1. Таким образом, приближение по недостатку будет √2 ≈ 1,414, а по избытку √2 ≈ 1,415.
Но примеры, рассмотренные выше, это положительные числа. А так ли обстоит дело при приближении отрицательных чисел. Если взять число –√2 = –1,414213..., то его приближением по избытку до тысячных долей будет –1,414, так как это число больше, чем –√2. А вот приближением по недостатку будет –1,415, так как это число меньше, чем –√2.
3,84
Объяснение:
Проводя различные измерения, решая уравнения графическим выполняя арифметические вычисления, часто получают приближенные значения, а не точные. Например, при вычислении корня числа может получиться бесконечная непериодическая дробь (т. е. иррациональное число). Кроме того, существуют бесконечные периодические дроби, использовать которые в вычислениях также неудобно.
Поэтому числа, являющиеся бесконечными десятичными дробями или конечными, но имеющими множество знаков после запятой, принято округлять.
Когда округление выполняется в большую сторону, то говорят о приближении по избытку. Когда округление выполняется в меньшую сторону, то говорят о приближении по недостатку.
Полученное при округлении число называют приближенным по недостатку или избытку с определенной точностью. Рассмотрим несколько примеров приближения.
Число π является бесконечной дробью 3,1415926535... Обычно его округляют с точностью до 0,01. Это значит, что после запятой оставляют только два знака. При приближении по избытку получится 3,15. При приближении по недостатку получится 3,14.
Для числа π обычно используют приближение по недостатку, так как согласно правилу округления положительные числа округляются в большую сторону, если первая отбрасываемая цифра 5 или больше пяти. Так как у числа π третья цифра после запятой — это 1, то округление выполняется в меньшую сторону, то есть для расчетов выполняется приближение по недостатку.
Однако, несмотря на правила округления, имеют право быть приближения как по недостатку, так и по избытку.
Если выполнять приближение числа π с точностью до 0,0001, то по избытку получим π ≈ 3,1416, а по недостатку π ≈ 3,1415.
Рассмотрим иррациональное число √2, которое равно 1,414213... . Вычислим его приближение по недостатку и по избытку с точностью до 0,001. Поскольку приближение выполняется до тысячных долей, то у числа надо оставить три знака после запятой. При приближении по недостатку просто отбрасываются все цифры после третьей после запятой. При приближении по избытку цифры после третьей после запятой отбрасываются, а третья цифра увеличивается на 1. Таким образом, приближение по недостатку будет √2 ≈ 1,414, а по избытку √2 ≈ 1,415.
Но примеры, рассмотренные выше, это положительные числа. А так ли обстоит дело при приближении отрицательных чисел. Если взять число –√2 = –1,414213..., то его приближением по избытку до тысячных долей будет –1,414, так как это число больше, чем –√2. А вот приближением по недостатку будет –1,415, так как это число меньше, чем –√2.
Так как функция косинус по модулю не превосходит единицы в поле действительных чисел, то выбираем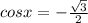
Далее решаем это уравнение:
По условию нужно найти корни на промежутке![[-\frac{7\pi}{2}; -2\pi]](/tpl/images/1359/8515/36df4.png) .
.
Это можно сделать несколькими например, с неравенства:
Рассмотрим случай, когда 5 имеет знак "плюс":
Очевидно, что из целых k подходит k = -2.
Теперь рассмотрим случай, когда 5 имеет знак "минус":
k = -1 нам подходит.
Теперь подставляем полученные k в серию корней:
1) Когда плюс - k = -2, т. е.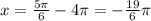
2) Когда минус - k = -1, т. е.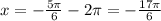
ответ: а)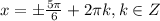
б)