F (x) = логарифм 3 степеня х
Знайдіть f(2) + f(½).

Нехай х км/год - швидкість першого пішохода, у км/ год - другого.
тоді:
1. якщо пройшли порівну, то по 15 км, отже 15/х - час першого, 15/у - час другого, але
15/х-15/у=1,25 (1 год 15 хв=1,25)
2. вийшли одночасно, отже х+у - швидкість зближення.
3(х+у)=30
Одержимо ситему
{15/х-15/у=1,25
{3(х+у)=30

{15/х-15/у=1,25
{х+у=10

{15/х-15/у=1,25
{х=10-у

15/(10-у)-15/у=1,25
15у-15(10-у)=1,25у(10-у)
15у-150+15у=12,5у-1,25у²

1,25у²+17,5у-1,50=0
у²+14у-120=0
за т. Вієта
у1у2=-120
у1+у2=-14
у1=-20 - не задовольняє, бо швидкість не може бути <0
у2=6

отже швидкість другого пішохода 6 км/год.
х=10-6=4 км/год швидкість першого пішохода

ответ:Объяснение:1 Запишем2 Умножим на 1

Но мы представим 1 как дробь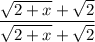 , такое действие еще называют домножением на сопряжённое

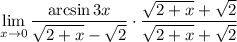
3 Соберем все в одну дробь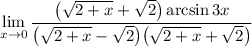

4 Заметим в знаменателе разность квадратов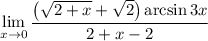

где

5 Упростим знаменатель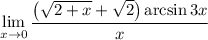

6 Представим дробь как произведение7 Представим предел произведения как произведение пределов8 Посчитаем первый предел9 Так как то мы можем заметить в пределе на 10 Умножим выражение пол пределом на 1

Но 1 мы представим в виде

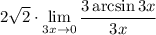
11 Вынесем константу (3) за предел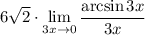

12 Имеем первый замечательный предел, он равен 1ОТВЕТ