Вопрос сформулирован некорректно. Единственное неравенство в условии F'(x)≤0. Другого, которое нужно решить, в условии нет.
Задача решена в следующей формулировке :
F(x)=tg8x-0,75x. Решите неравенство F'(x)≤0 .
Значение производной ≥7,25, следовательно, оно не может быть отрицательным или равным нулю.
ответ : ∅
Неравенство не имеет решений
Объяснение:
Функция
F(x) = tg 8x - 0.75x
Производная
F'(x) ≤ 0
Знаменатель производной 4cos² 8x > 0 и cos² 8x ∈ (0; 1]
Тогда
32 - 3 cos² 8x ≤ 0
3cos² 8x ≥ 32
cos²8x ≥ , a 32/3 > 1 чего быть не может, так как для любого угла сos²α ∈ [0; 1].
Поэтому неравенство F'(x) ≤ 0 решений не имеет.
Вопрос сформулирован некорректно. Единственное неравенство в условии F'(x)≤0. Другого, которое нужно решить, в условии нет.
Задача решена в следующей формулировке :
F(x)=tg8x-0,75x. Решите неравенство F'(x)≤0 .
Значение производной ≥7,25, следовательно, оно не может быть отрицательным или равным нулю.
ответ : ∅
Неравенство не имеет решений
Объяснение:
Функция
F(x) = tg 8x - 0.75x
Производная
F'(x) ≤ 0
Знаменатель производной 4cos² 8x > 0 и cos² 8x ∈ (0; 1]
Тогда
32 - 3 cos² 8x ≤ 0
3cos² 8x ≥ 32
cos²8x ≥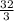
, a 32/3 > 1 чего быть не может, так как для любого угла сos²α ∈ [0; 1].
Поэтому неравенство F'(x) ≤ 0 решений не имеет.