F(x)=x²+4/2-x знайдіть проміжки зростання та спадання функції

Разложим sin2x = 2 * sinx * cosx, а 1 = sin^2x + cos^2x, получим:

sin^2x + 2 * sinx * cosx +cos^2x = sinx + cosx;

sin^2x + 2 * sinx * cosx +cos^2x – sinx – cosx = 0;

(sinx + cosx) * (sinx + cosx -1) = 0;

Получим два уравнения:

sinx + cosx = 0;

sinx + cosx – 1 = 0;

Решим первое уравнение:

sinx + cosx = 0;

sinx/cosx + 1 = 0;

tgx + 1 = 0;

tgx = -1;

x = -п/4 + п * k, k принадлежит Z

Решим второе уравнение:

sinx + cosx – 1 = 0;

sinx/cosx + 1 – 1/cosx = 0;

tgx + 1 = 1/cosx;

(tgx + 1)^2 = (1/cosx)^2;

tg^2x + 2 * tgx + 1 = 1/cos^2x;

tg^2x + 2 * tgx + 1 = tg^2x + 1;

tg^2x + 2 * tgx + 1 – tg^2x – 1 = 0;

2 * tgx = 0;

tgx = 0;

x = п * k, k принадлежит Z.

ответ: x = -п/4 + п * k, k принадлежит Z; x = п * k, k принадлежит Z

Распределительный (дистрибутивный) закон умножения относительно сложения: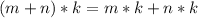

Объяснение:

Также помним и об остальных законах сложения и умножения:

Переместительный (коммутативный) закон сложения:   Сумма не меняется от перестановки её слагаемых.

Переместительный (коммутативный) закон умножения: Произведение не меняется от перестановки его сомножителей.

Сочетательный (ассоциативный) закон сложения:    Сумма не зависит от группировки её слагаемых.

Сочетательный (ассоциативный) закон умножения:                        Произведение не зависит от группировки его сомножителей.