Фигура 1 1) (2; -3), (2; -2), (4; - 2), (4; -1), (3; 1), (2; 1), (1; 2), (0; 0), (-3; 2), (4; 5), (0; 8), (2; 7), (6; 7), (8; 8), (10; 6), (10; 2), (7; 0), (6; 2), (6; -2), (5; - 3), (2; -3). 2) (4; -3), (4;5), (3; -9), (0; -8), (1; - 5), (1; -4), (0; - 4), (0; -9), (-3; -9), (-3; -3), (-7; -3), (-7; -7), (-8; - 7), (-8; -8), (- 11; -8), (- 10; -4), (- 11; -1), (- 14; -3), (-12; 1), (- 11;2), (-8;4),(4;5). 3) Глаза: (2; 4), (6; 4).

Фигура 2

1) (2; 7), (0; 5), (-2; 7), (0; 8), (2; 7), (- 4; -3), (4; 0), (11; - 2), (9; -2), (11; -3),

(9; -3), (5; -7), (- 4; - 3). 2) Клюв: (-4; 8), (- 2; 7), (- 4; 6).

3) Kрыло: (1-3), (4; - 2), (7; -3), (4; - 5), (1; - 3).

4) Глаз: (0; 7)

Показать ответ

Ответ:

АннаФилип270406

06.10.2022 09:10

ответ: 25

Объяснение:

Рассмотрим треугольник со сторонами 16 и 12, в нем неизвестная сторона будет равна: х=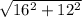 $\sqrt{16^{2}+12^{2}$ =20

Воспользуемся свойством высоты в прямоугольном треугольнике, проведенной из прямого угла:

Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных ему, каждый из которых подобен данному.

Используя отношение найдем второй катет большого треугольника через маленькие:

$\frac{20}{x}=\frac{16}{12}$ , где х=15

Найдем гипотенузу через формулы площади треугольника.

S=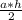 $\frac{a*h}{2}$ , где а=16+х, h=12

а=16+х-гипотенуза

S=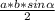 $\frac{a*b*sin\alpha }{2}$ , где sin90=1, а=20, b=15.

S=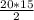 $\frac{20*15}{2}$ =150

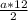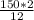150= $\frac{a*12}{2}$ , а= $\frac{150*2}{12}$ =25.

0,0(0 оценок)

Ответ:

Arinka2184

20.03.2023 12:06

Пусть ширина листа (сторона квадрата) равна b=х см. После того, как от прямоугольного листа картона отрезали квадрат, длина оставшегося прямоугольника стала равна a=16-х см.
Площадь прямоугольника равна: S=a*b=60 см²
Составим и решим уравнение:
х(16-х)=60
16х-х²=60
х²-16х+60=0
D=b²-4ac=(-16)²-4*1*60=256-240=16 (√16=4)
х₁= $\frac{-b+ \sqrt{D} }{2a}$ = $\frac{-(-16)+4)}{2*1} = \frac{20}{2}$ = 10
х₂= $\frac{-b- \sqrt{D} }{2a}$ = $\frac{-(-16)-4)}{2*1} = \frac{12}{2}$ = 6
ОТВЕТ: ширина листа равна 10 см; ширина листа равна 6 см.

По теореме Виета:
х²-16х+60=0
х₁+х₂=16
х₁*х₂=60
х₁=10
х₂=6

Проверим:
Ширина листа равна 10 см, длина 16 см.
Вырезанный квадрат со стороной а=10 см.
Ширина оставшегося прямоугольника равна 10 см, длина 16-10=6 см. Площадь равна: S=10*6=60 см².

Ширина листа равна 6 см, длина 16 см.
Вырезанный квадрат со стороной а=6 см.
Ширина оставшегося прямоугольника равна 6 см, длина 16-6=10 см. Площадь равна: S=6*10=60 см².

0,0(0 оценок)

Популярные вопросы: Алгебра