Объяснение:Дана функція є періодична.Знайдем похідну даної функції. y=cos(x) -sin(x).Похідна даної функції має вигляд: -sin(x)-cos(x)Знайдем критичні точки функції , коли похідна рівна 0. -sin(x) - *cos(x) = 0; → sin(x) + √3*cos(x)=0;(sin(x)/cos(x)) + √3*(cos(x)/cos(x))=0/cos(x);tg(x)+√3=0; → tg(x)= -√3; → x=arctg(-√3);x= -(π/3) + πn, де n ∈ Z.Знаходим значення функції в критичних точкахx= -(π/3); → y=cos(-π/3) - √3*sin(π/3)=(1/2) -√3*(-√3/2)=1/2 + 3/2=2;x=(2π/3); → y=cos(2π/3) -√3*sin(2π/3)==-(1/2) - √3*(√3/2)= -1/2 - 3/2=-2.Відповідь: найбільше значення функції у=2;найменше значення функції у=-2.
Пусть АВСD - данная трапеция, AB || CD; AB = AD;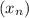 - арифметическая прогрессия.
- арифметическая прогрессия.
Пусть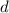 - разность прогрессии, AB =
- разность прогрессии, AB = 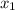 По формуле
По формуле 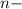 ого члена имеем: BC =
ого члена имеем: BC = 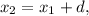 CD =
CD = 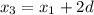
Периметр трапеции равен: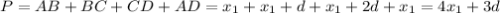 , т.е.
, т.е.
Опустим высоту BK = AD =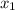 ⇒ ABKD - квадрат ⇒ KD =
⇒ ABKD - квадрат ⇒ KD = 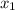 ⇒ CK = CD - KD =
⇒ CK = CD - KD = 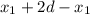 =
=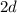 .
.
В ΔВКС (∠К = 90°) по теореме Пифагора: ВС² = ВК² + СК² =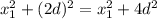 ⇒
⇒ 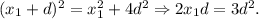
Имеем систему:
Тогда AD = AB = 24 дм, BC = 24 + 16 = 40 дм, CD = 24 + 2 · 16 = 56 дм.
ОТВЕТ: 24 дм; 24 дм; 40 дм; 56 дм.
Доп. вопросы:
1. d = 16
2. Теорема Пифагора
3. Неравенство треугольника: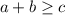
4. Сторона основания (CD).