Функцію задано формулою f(x)=x^-3/7. Порівняйте f(2.8) і f(3.7).

да

Объяснение:

Пусть числитель равен х, тогда знаменатель (х +1). Исходная дробь будет выглядеть как х / (х + 1). Измененная дробь — х / (х + 3).

Разность дробей составляет 1/4. Получаем уравнение:

х / (х + 1) - х / (х + 3) = 1 / 4;

4 * х * (х + 3) - 4 * х * (х + 1) = (х +1) * (х + 3);

4 * х² + 12 * x - 4 * x² - 4 x = x² + 4 * x + 3;

x² - 4 * x +3 = 0;

D = 16 - 4 * 1 * 3 = 16 - 12 = 4;

х1 = (4 - 2) / 2 = 1;

х2 = (4 + 2) / 2 = 3.

Задача имеет два решения:

1) х1 = 1;  y1 = x1 + 1 = 2.

Первая дробь, удовлетворяющая условиям — 1/2.

Проверка:

1/2 - 1/4 = 1/4.

2) х2 = 3; y2 = x2 + 1 = 4.

Вторая дробь, удовлетворяющая условиям — 3/4.

Проверка:

3/4 - 3/6 = 1/4.

   ОДЗ: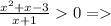     [-2,3;  -1)∪[1,3; +∞)                  

Так как основание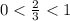  , то для показателей степеней справедливо неравенство:

              -                              +                             -                            +

-2 -1                          2

                                     [-2;   -1)                  и                               [2;  +∞)

                                         удовлетворяет ОДЗ  

ответ:  [-2;   -1)∪[2;  +∞)