Функцію задано формулою у = 1\2 (дробь)(4х – 6) -3(0,25х – 2). Знайти значення аргументу, при якому відповідне значення функції дорівнює 4.
Не виконуючи побудов, знайти точки перетину з координатними осями графіка функції у = - 1\4(дробь)х + 5.
Побудувати графік функції у = 1\6(дробь)х – 2.
Заметим, что при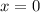 левая и правая часть уравнения обращается в 0. Значит, число 0 является корнем этого уравнения.
левая и правая часть уравнения обращается в 0. Значит, число 0 является корнем этого уравнения.
Предположим, что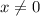 . Тогда, мы можем разделить обе части равенства на
. Тогда, мы можем разделить обе части равенства на  . Получим:
. Получим:
Рассмотрим левую часть.
Вспомним, что функция вида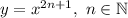 является возрастающей на всей области определения, то есть на множестве действительных чисел. Тогда и функция
является возрастающей на всей области определения, то есть на множестве действительных чисел. Тогда и функция 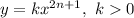 является возрастающей. Сумма возрастающих функций также является возрастающей.
является возрастающей. Сумма возрастающих функций также является возрастающей.
Применительно к данному уравнению можно записать: функции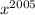 ,
, 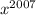 , ...,
, ..., 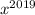 возрастают, тогда и функции
возрастают, тогда и функции 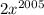 ,
, 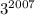 , ...,
, ..., 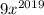 также возрастают, а значит возрастает и их сумма.
также возрастают, а значит возрастает и их сумма.
Таким образом, функция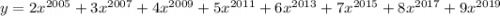 возрастает. Это означает, что каждое свое значение она принимает только в одной точке.
возрастает. Это означает, что каждое свое значение она принимает только в одной точке.
Следовательно, уравнение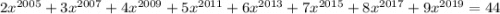 может иметь не более одного решения.
может иметь не более одного решения.
Решение уравнения легко подбирается: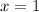 . Действительно, сумма коэффициентов в левой части уравнения равна 44:
. Действительно, сумма коэффициентов в левой части уравнения равна 44:
В силу сказанного выше, других корней у уравнения нет.
ответ: 0; 1
Объяснение:
f(x) = x^2021 + a - заданная прямая функция.
f^(-1) (x) = корень 2021 степени из (x-a) - обратная функция.
Обратная функция имеет график, симметричный данному относительно прямой y = x.
Графики функции и обратной могут пересекаться только на прямой y = x.
Это значит, что функция сама должна пересекаться с прямой y = x.
Решаем уравнение и находим х при любом параметре а:
y = x^2021 + a = x
x = x^2021 + a
x^2021 - x + a = 0
Любой многочлен нечётной степени всегда имеет хотя бы один корень.
Поэтому при любом значении а будет хотя бы одно решение.