Функция f(x)=y определена на всей числовой прямой и является четной функцией с периодом равным 6. На отрезке [0;3] функция задана формулой f(x)=x^2 - x - 2. Определите количество нулей этой функции на отрезке [-5;4]
Y=(9x+1) / (9x^2+x) ОДЗ: 9x^2+x неравен 0 преобразуем знаменатель: x(9x+1) неравен 0 y=(9x+1) / (x(9x+1)) x неравен 0 или 9x+1 неравен 0 сократим 9х+1, получится функция вида y=1/x. x неравен -1/9 составим таблицу: x=1 y=1 x=2 y=0,5 x=4 y=0,25 x=-1 y=-1 x=-1/9 y=-9 ( эта точка на графике будет не закрашена,т.е.выколотая) x=-2 y=-0,5 дальше строишь гиперболу. и через выколотую точку и вторую ветвь проводишь прямую. далее поставляешь в y=kx значение y и x: -9=k*(-1/9) решаешь, и получается k=81. вроде,так.
Максимум в точке х =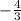
(для записи 
)
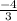Минимум в точке х = -1
Объяснение:
f(x)=2x^3+7x^2+8x+4
Область определения:
Х∈R
f(x)=2x^3+7x^2+8x+4, Х∈R
Определим производную f:
f(x) = 2x^3+7x^2+8x+4
f'(x) = d/dx (2x^3+7x^2+8x+4)
f'(x) = d/dx(2x^3) + d/dx(7x^2) + d/dx(8x) + d/dx(4)
f'(x) = 2*3x^2 + 7*2x+8+0
f'(x) = 6x^2+14x+8
f'(x) = 6x^2+14x+8, Х∈R
Представим f'(x) = 0
0=6x^2+14x+8
Решим ур-е относительно Х
6x^2+14x+8=0 | :2
3x^2+7x+4=0
D=b2-4ac = 7^2-4*3*4 = 1
x1,2= -b+-D/2a = -7+-1/2*3
x1= - 4/3
х2= -1
X∈(-∞;- 4/3)
X∈(- 4/3;-1)
max: - 4/3
min: -1
преобразуем знаменатель: x(9x+1) неравен 0
y=(9x+1) / (x(9x+1)) x неравен 0 или 9x+1 неравен 0
сократим 9х+1, получится функция вида y=1/x. x неравен -1/9
составим таблицу:
x=1 y=1
x=2 y=0,5
x=4 y=0,25
x=-1 y=-1
x=-1/9 y=-9 ( эта точка на графике будет не закрашена,т.е.выколотая)
x=-2 y=-0,5
дальше строишь гиперболу. и через выколотую точку и вторую ветвь проводишь прямую.
далее поставляешь в y=kx значение y и x:
-9=k*(-1/9)
решаешь, и получается k=81. вроде,так.