Линейное уравнение с двумя переменными имеет вид: ах + by + c = 0. Графиком данного уравнения, в общем виде, является прямая. Если только один коэффициент при переменной отличен от нуля, то графиком такого уравнения будет прямая, параллельная одной из осей координат. Если оба коэффициента при переменных равны 0, и с = 0, то графиком будет вся координатная плоскость. А если при данных условиях с ≠ 0, то графиком будет пустое множество. Если же оба коэффициента при переменных отличны от 0, то прямая может быть абсолютно любой.
ответ: прямая; прямая параллельная оси координат; координатная плоскость; ничего (пустое множество)
Возможно, существует и другой метод доказательства, но я буду использовать метод от противного.
Итак, нужно доказать, что , то есть
Перепишем наше равенство, переместив все в левую часть:
1) Предположим, что (при этом подразумевая, что )
Тогда получаем следующее:
Далее смотрим: слева неотрицательное выражение всегда, а справа может быть и отрицательное, но у нас по условию дано, что для любых действительных чисел равенство выполняется, а здесь это далеко не так (на языке математики запись такая: )
Возможно, это не очень явно, поэтому вспомним, что по предположению , и доделаем:
А это прямо яркий пример противоречия: предположив, что , мы получили .
Из этого следует, что , но и из предположенного же уже следует, что .
Вообще, по идее, этого уже достаточно, ну на всякий случай посмотрим ещё:
2) Предположим, что (при этом )
И тогда уже точно исходя из пунктов 1) и 2), получаем
Линейное уравнение с двумя переменными имеет вид: ах + by + c = 0. Графиком данного уравнения, в общем виде, является прямая. Если только один коэффициент при переменной отличен от нуля, то графиком такого уравнения будет прямая, параллельная одной из осей координат. Если оба коэффициента при переменных равны 0, и с = 0, то графиком будет вся координатная плоскость. А если при данных условиях с ≠ 0, то графиком будет пустое множество. Если же оба коэффициента при переменных отличны от 0, то прямая может быть абсолютно любой.
ответ: прямая; прямая параллельная оси координат; координатная плоскость; ничего (пустое множество)
Возможно, существует и другой метод доказательства, но я буду использовать метод от противного.
Итак, нужно доказать, что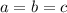 , то есть
, то есть
Перепишем наше равенство, переместив все в левую часть:
1) Предположим, что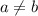 (при этом подразумевая, что
(при этом подразумевая, что 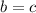 )
)
Тогда получаем следующее:
Далее смотрим: слева неотрицательное выражение всегда, а справа может быть и отрицательное, но у нас по условию дано, что для любых действительных чисел равенство выполняется, а здесь это далеко не так (на языке математики запись такая: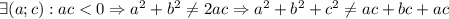 )
)
Возможно, это не очень явно, поэтому вспомним, что по предположению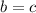 , и доделаем:
, и доделаем:
А это прямо яркий пример противоречия: предположив, что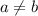 , мы получили
, мы получили 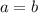 .
.
Из этого следует, что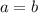 , но и из предположенного же
, но и из предположенного же 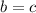 уже следует, что
уже следует, что 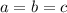 .
.
Вообще, по идее, этого уже достаточно, ну на всякий случай посмотрим ещё:
2) Предположим, что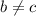 (при этом
(при этом 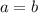 )
)
И тогда уже точно исходя из пунктов 1) и 2), получаем