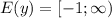Приклад:
Розв'язати систему рівнянь: {x−2y=3,5x+y=4.
1) З першого рівняння системи виражаємо змінну x через змінну y.
Отримуємо: x−2y=3,x=3+2y;
2) Підставимо отриманий вираз замість змінної x у друге рівняння системи:
5⋅x+y=4,5⋅(3+2y)+y=4;
3) Розв'яжемо утворене рівняння з однією змінною, знайдемо y:
5⋅(3+2y)+y=4,15+10y+y=4,10y+y=4−15,11y=−11,|:11y=−1¯¯¯¯¯¯¯¯¯¯¯.
4) Знайдемо відповідне значення змінної x, підставивши значення змінної y, у вираз знайдений на першому кроці:
x=3+2⋅y,x=3+2⋅(−1),x=3−2,x=1¯¯¯¯¯¯¯¯.
5) Відповідь: (1;−1) .
Объяснение:
это решить линейные уравнения без черчежей
Графиком данной функции является парабола.
Область значения функции- это те числа, значение которых может принимать "y".
означает, то что параболу сдвинули на две единицы измерения вправо относительно оси OY.
означает то, что параболу сдвинули вниз на одну единицу измерения вниз относительно OX.
Исходя из это можно узнать, что координаты вершины стали
Коэффициент "a" больше нуля, следовательно ветви параболы направлены вверх. А это значит, наименьшее значение функция будет принимать в вершине.
ответ:
Приклад:
Розв'язати систему рівнянь: {x−2y=3,5x+y=4.
1) З першого рівняння системи виражаємо змінну x через змінну y.
Отримуємо: x−2y=3,x=3+2y;
2) Підставимо отриманий вираз замість змінної x у друге рівняння системи:
5⋅x+y=4,5⋅(3+2y)+y=4;
3) Розв'яжемо утворене рівняння з однією змінною, знайдемо y:
5⋅(3+2y)+y=4,15+10y+y=4,10y+y=4−15,11y=−11,|:11y=−1¯¯¯¯¯¯¯¯¯¯¯.
4) Знайдемо відповідне значення змінної x, підставивши значення змінної y, у вираз знайдений на першому кроці:
x=3+2⋅y,x=3+2⋅(−1),x=3−2,x=1¯¯¯¯¯¯¯¯.
5) Відповідь: (1;−1) .
Объяснение:
это решить линейные уравнения без черчежей
Графиком данной функции является парабола.
Область значения функции- это те числа, значение которых может принимать "y".
Исходя из это можно узнать, что координаты вершины стали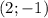
Коэффициент "a" больше нуля, следовательно ветви параболы направлены вверх. А это значит, наименьшее значение функция будет принимать в вершине.
ответ: