Функция y = f(x) – периодическая и четная, определена на всей числовой прямой. Период равен T = 6. На отрезке [–3; 3] функция задана формулой f(x) = x^2– 4. Найди количество нулей функции y = f(x) на отрезке [–6; 7].

Показать ответ

Ответ:

matveye234

26.12.2020 07:40

B₂=b₁*q
b₃=b₁*q²
b₄=b₁*q³

{b₁*q²+b₁*q³=36
{b₁*q+b₁*q²=18

{b₁(q²+q³)=36
{b₁(q+q²)=18

{b₁= 36
q²+q³
{b₁= 18
q+q²

36 = 18
  q²+q³ q+q²

36 = 2*18
q²+q³ 2(q+q²)

q²+q³=2(q+q²)
q²+q³=2q+2q²
q³+q²-2q²-2q=0
q³-q²-2q=0
q(q²-q-2)=0

q=0 - не подходит

q²-q-2=0
D=1+8=9
q₁=1-3=-1
2
q₂=1+3=2
2

При q=-1 b₁= 18
-1+(-1)²
b₁ = 18
0
q=-1 - не подходит

При q=2 b₁= 18
2+2²
b₁= 18
6
b₁=3

b₅=b₁*q⁴
b₅=3*2⁴
b₅=48
ответ: 48.

0,0(0 оценок)

Ответ:

122519

04.08.2020 22:35

$f(x)=\left\{\begin{array}{l}2^{x}\ ,\ \ x\leq 0\ ,\\-x^2\ ,\ \ 0$

Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .

$a)\ \ \lim\limits _{x \to 0-0}f(x)=\lim\limits _{x \to 0-0}2^{x}=1\ \ ,\ \ \ \lim\limits _{x \to 0+0}f(x)=\lim\limits _{x \to 0+0}(-x^2)=0\\\\\lim\limits _{x \to 0-0}f(x)\ne \lim\limits _{x \to 0+0}f(x)\ \ \Rightarrow$

При х=0 функция имеет разрыв 1 рода .

$b)\ \ \lim\limits _{x \to 2-0}f(x)=\lim\limits _{x \to 2-0}(-x^2)=-4\ ,\ \ \lim\limits _{x \to 2+0}f(x)=\lim\limits _{x \to 2+0}(x-6)=-4\\\\f(2)=(-x^2)\Big|_{x=2}-4\\\\\lim\limits _{x \to 2-0}f(x)=\lim\limits _{x \to 2+0}f(x)=f(2)=-4\ \ \ \Rightarrow$

При х=2 функция непрерывна.

$c)\ \ \lim\limits _{x \to 5-0}f(x)=\lim\limits _{x \to 5-0}(x-6)=-1\\\\\lim\limits _{x \to 5+0}f(x)=\lim\limits _{x \to 5+0}3^{\frac{4x}{x-5}}=3^{+\infty }=+\infty \ \ \ \Rightarrow$

При х=5 функция имеет разрыв 2 рода .

График функции нарисован сплошной линией.

На 1 рисунке нет чертежа функции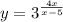 $y=3^{\frac{4x}{x-5}}$ при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .