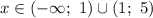Функция задана уравнением у = х^2 + 5х +4. а) В какой точке график данной функции пересекает ось OY?
b) Найдите точки пересечения графика функции с осью ОХ.
c) Запишите уравнение оси симметрии графика данной функции
d) Постройте график функции​

(x-4)(x-6) > 0

метод интервалов:     (x-4)(x-6) = 0
                                      х = 4     х = 6  (нули функции)

           +                                                                    +
/___/___/___/___/__46_/___/___/___/___/_     
                                                   -
ответ:        ( - оо ; 4 )  ∨ ( 6 ; + оо)

x² - 10x  ≤ -9x + 1 - x²
x² - 10x  + 9x - 1 + x² ≤ 0
2x² - х - 1 ≤ 0
D = 1 - 4*2*(-1) = 9  √D=3
х2 = 1 + 3      = 1
         4
х2 =  1 - 3      = - 0,5
           4

      +                                                   +
- 0,51     
                                                        -

ответ:       [  - 0,5 ; 1 ]

Первый

Анализируем: здесь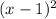 — неотрицательная величина; имеем: при умножении неотрицательной величины с другим выражением мы можем получить отрицательное число, если второе выражение будет отрицательным, а первое — не равным нулю:

Итак, общим ответом будет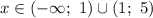

Второй

Решим неравенство методом интервалов:

1) Найдем нули данного выражения:

2) ОДЗ: все числа

3) Начертим координатную прямую и отметим нули данного выражения выколотыми точками (так как неравенство строгое) и определим знак на каждом участке и объединим участок (участки), содержащие знак "минус" (см. вложение).

Итак, общим ответом будет