Объяснение:
1)
из 5 имеющихся букв нужно составить слово состоящее из 3 букв
последовательность букв имеет значение
всего может быть составлено слов по 3 буквы из имеющихся 5 букв 5*4*3 = 60
нас устраивает только одно из 60 - ти
искомая вероятность р = 1/60 - это ответ
2)
a)
зеленых в корзине 5, всех в корзине 5+15=20
вероятность что трижды вытащат зеленое яблоко 5/20 *4/19 * 3/18 = 1/(19*6) =1/114 - это ответ
б)
вероятность что зеленое было первым а остальные два красные
5/20*15/19*14/18
вероятность что зеленое было вторым а остальные два красные
15/20*5/19*14/18
вероятность что зеленое было третьим а остальные два красные
15/20*14/19*5/18
искомая вероятность
5/20*15/19*14/18 * 3 = 1/4*5/19*7/9 = (5*7)/(4*9*19) = 35/684 - это ответ
3)
а)
вероятность вытащить два белых или два черных если шары возвращаются
5/15*5/15 + 10/15*10/15 = (25+100)/225 = 125/225 = 5/9 - это ответ
вероятность вытащить два белых или два черных если шары не возвращаются
5/15*4/14 + 10/15*9/14 = (20+90)/210 =110/210 = 11/21 - это ответ
в)
вероятность вытащить два белых (и ни одного черного) если шары не возвращаются
p= 5/15*4/14 = 20/210 = 2/21
вероятность вытащить из двух хотя бы один черный если шары не возвращаются равна обратной вероятности от предыдущего события
q=1-p = 1 - 5/15*4/14 = 1 - 2/21 = 19/21 - это ответ
Первый
Решение ищем как сумму общего решения однородного уравнения, соответствующего данному неоднородному, и частного решения данного неоднородного уравнения.
Составим однородное уравнение, соответствующее данному неоднородному:
Решаем уравнение с разделяющимися переменными:
Общее решение однородного уравнения:
Частное решение ищем в виде .
Найдем производную:
Подставим в уравнение:
Условие равенства левой и правой частей:
Частное решение неоднородного уравнения:
Искомое решение:
Второй
Решение ищем в виде произведения двух ненулевых функций . Тогда .
Пусть сумма первого и третьего слагаемого в левой части равна нулю:
Тогда второе слагаемое в левой части равно правой части:
Интеграл вычислим отдельно. Будем использовать интегрирование по частям: (не записывая произвольную константу):
Таким образом:
Искомая функция:
Объяснение:
1)
из 5 имеющихся букв нужно составить слово состоящее из 3 букв
последовательность букв имеет значение
всего может быть составлено слов по 3 буквы из имеющихся 5 букв 5*4*3 = 60
нас устраивает только одно из 60 - ти
искомая вероятность р = 1/60 - это ответ
2)
a)
зеленых в корзине 5, всех в корзине 5+15=20
вероятность что трижды вытащат зеленое яблоко 5/20 *4/19 * 3/18 = 1/(19*6) =1/114 - это ответ
б)
вероятность что зеленое было первым а остальные два красные
5/20*15/19*14/18
вероятность что зеленое было вторым а остальные два красные
15/20*5/19*14/18
вероятность что зеленое было третьим а остальные два красные
15/20*14/19*5/18
искомая вероятность
5/20*15/19*14/18 * 3 = 1/4*5/19*7/9 = (5*7)/(4*9*19) = 35/684 - это ответ
3)
а)
вероятность вытащить два белых или два черных если шары возвращаются
5/15*5/15 + 10/15*10/15 = (25+100)/225 = 125/225 = 5/9 - это ответ
б)
вероятность вытащить два белых или два черных если шары не возвращаются
5/15*4/14 + 10/15*9/14 = (20+90)/210 =110/210 = 11/21 - это ответ
в)
вероятность вытащить два белых (и ни одного черного) если шары не возвращаются
p= 5/15*4/14 = 20/210 = 2/21
вероятность вытащить из двух хотя бы один черный если шары не возвращаются равна обратной вероятности от предыдущего события
q=1-p = 1 - 5/15*4/14 = 1 - 2/21 = 19/21 - это ответ
Первый
Решение ищем как сумму общего решения однородного уравнения, соответствующего данному неоднородному, и частного решения данного неоднородного уравнения.
Составим однородное уравнение, соответствующее данному неоднородному:
Решаем уравнение с разделяющимися переменными:
Общее решение однородного уравнения:
Частное решение ищем в виде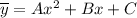 .
.
Найдем производную:
Подставим в уравнение:
Условие равенства левой и правой частей:
Частное решение неоднородного уравнения:
Искомое решение:
Второй
Решение ищем в виде произведения двух ненулевых функций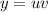 . Тогда
. Тогда 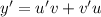 .
.
Пусть сумма первого и третьего слагаемого в левой части равна нулю:
Тогда второе слагаемое в левой части равно правой части:
Интеграл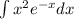 вычислим отдельно. Будем использовать интегрирование по частям:
вычислим отдельно. Будем использовать интегрирование по частям: 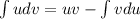 (не записывая произвольную константу):
(не записывая произвольную константу):
Таким образом:
Искомая функция: