График движения автомобиля из одного города в другой и обратно
дано. Найдите, сколько километров он проехал всего А) 260 км
B) 240 км
C) 250 км
D) 230 км
E) 270 км

График движения автомобиля из одного города в другой и обратно дано. Найдите, сколько километров он

Показать ответ

Ответ:

olesjaozs5is

17.05.2021 16:55

Для решения задачи воспользуемся законом Гука, который гласит о том, что Сила упругости, возникающая в теле при его деформации(растяжении) прямо пропорциональна этой деформации(удлинению) и направлена противоположно этой деформации(растяжению). В нашем случае дано удлинение пружины.

Fупр=-kΔl, где k - коэффицент жесткости пружины, Δl - удлинение пружины.

Знак минуса можем отбросить, он лишь показывает то, что сила противоположно направлена деформации пружины

Тогда

Fупр(1)=kΔl => k = Fупр/Δl k = 40Н/0,02м=2000 Н/м

Решим задачу с потенциальной энергии деформированного тела.

Eп=kΔl^2 / 2 , где k - коэффицент жесткости, Δl^2 - квадрат удлинения.

Формула работы следующая: A=-(E2-E1) Знак минуса означает, что работа отрицательна.

E1=2000Н * (0.02 м)^2 = 0,4 Дж

E2=2000Н * (0,06м)^2 = 3,6 Дж

A = -(3,6Дж-0,4Дж)= 3,2 Дж

ответ: 3,2 Дж

0,0(0 оценок)

Ответ:

danilkuzin201

16.01.2021 22:11

$1)\quad f'(x)=2-2x$

Уравнение касательной имеет вид

y=f'(1)(x-1)+f(1)

y=(2-2*1)*(x-1)+(2*1-1^2)

y=1

Уравнение нормали будет перпендикулярно уравнению касательной в данной точке.

В данном случае будет иметь вид х=1. Так как эта прямая перпендикулярна касательной в точке х=1 прямой у=1.

$2)\quad f'(x)=\cos x$

Уравнение касательной имеет вид

$y=f'(\frac{\pi}{4})*(x-\frac{\pi}{4})+\sin\frac{\pi}{4}$

$y=\frac{\sqrt{2}}{2}*(x-\frac{\pi}{4})+\frac{\sqrt{2}}{2}$

$y=\frac{\sqrt{2}}{2}*x-\frac{\sqrt{2}\pi}{8}+\frac{\sqrt{2}}{2}$ - это будет уравнение касательной.

Чтобы найти уравнение нормали надо взять прямую, перпендикулярную данной в точке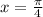 $x=\frac{\pi}{4}$ . Угловой коэффициент у такой прямой будет отличаться от исходной прямой тем, что будет равен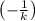 $\left(-\frac{1}{k}\right)$

В данном случае прямая будет иметь вид

$y=-\frac{1}{\frac{\sqrt{2}}{2}}x+b$

Или

$y=-\sqrt{2}x+b\quad(*)$

Так как проходит через точку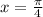 $x=\frac{\pi}{4}$ и значение нормали равно значению самой исходной функции, то есть 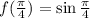$f(\frac{\pi}{4})=\sin\frac{\pi}{4}$ , то есть 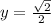$y=\frac{\sqrt{2}}{2}$ . Подставим эти значения в уравнение (*).