Х: 49, 43, 46, 38, 48, 44, 44, 43, 40, 41, 39, 44, 43, 44, 46, 50, 51, 38, 38, 43, 39 Обчислити розмах, медіану, моду. Побудувати варіаційний ряд розподілу
частот. Побудувати график (полігон) розподілу частот.

Показать ответ

Ответ:

Тэт11

12.05.2020 06:22

По свойству арифметической прогрессии:

a_n=a_1+(n-1)d , где d-это разность арифметической прогрессии.

Из условий можно составить систему из 2х уравнений:

$\left \{ {{a_2=a_1+d} \atop {a_{28}=a_1+27 \cdot d}} \right.$

нам известно что: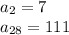 $a_2=7 \\a_{28}=111$

Подставляем и получаем:

$\left \{ {{7=a_1+d} \atop {111=a_1+27 \cdot d}} \right.$

Решаем систему: из 1го уравнения выражаем ну хотя бы d:

d=7-a_1

Подставляем во второе:

$111=a_1+27 \cdot (7-a_1) \\ 111=a_1+189-27a_1 \\26a_1=189-111 \\26a_1=78 \\ a_1=3$

Теперь найдем d:

d=7-3=4

Разность прогрессии нашли, она равна 4.

Теперь сумма первых 28 членов:

По формуле сумма n членов арифметической прогрессии равна:

$S_n=\frac{a_1+a_n}{2}\cdot n$ или $S_n=\frac{2\cdot a_1+(n-1) \cdot d}{2}\cdot n$

Можно пользоваться любой формулой результат будет одинаковый, но воспользуемся все таки первой, она проще для вычислений и 28 член прогрессии нам известен.

$S_{28}=\frac{3+111}{2} \cdot 28=114 \cdot 14=1596$

(можно убедиться, что вторая формула даст такой же результат).

разность арифметической прогрессии d = 4

Сумма первых 28 членов прогрессии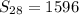 $S_{28}=1596$

0,0(0 оценок)

Ответ:

ВалераГущина

07.03.2023 02:00

$6)10x(x-1)(x+1)^{2}-5\\\\10x^{2}-10xx^{2}+2x+1-5\\\\10x^{2}-10x-x^{2}-2x+40\\\\9x^{2}-12x+40\\\\9x^{2}-12x+4=0\\\\D=(-12)^{2}-4*9*4=144-144=0\\\\x=\frac{12}{18}=\frac{2}{3}\\\\9(x-\frac{2}{3})^{2} 0\\\\(x-\frac{2}{3})^{2}0\\\\x\in(-\infty;\frac{2}{3})\cup(\frac{2}{3};+\infty)$

$8)\frac{x-1}{4}-\frac{2x-3}{2}<\frac{x^{2}+3x }{8}\\\\2(x-1)-4(2x-3)<x^{2}+3x \\\\2x-2-8x+12<x^{2}+3x\\\\x^{2}+3x+6x-100\\\\x^{2}+9x-100\\\\(x-1)(x+10)0$