Спочатку розглянемо скільки можна утворити чотирицифрових чисел з цифр 0, 2, 3, 4, 5, 6, якщо кожна з цифр не повторюється
(0 не можна ставити на першу позицію), значить варіантів утворити число буде 5*5*4*3=300 (будь яку ненульову цифру на першу позицію, на другу позицію будь-яку з решти 5-ти цифр (уже включаючи 0 для вибору) після вибору першої, на третю будь-яку з решти 4-ох після вибору перших двох, і на четверту позицію відповідно 3 варіанта вибору)
Тепер розглянемо скільки можна утворити чотирицифрових чисел з цифр 0, 2, 3, 4, 5, 6, у яких остання цифра 3:
(0 і 3 не можна ставити на першу позицію, 3 на останній позиції, не можна повторюватися), 4*4*3*1=48
Аналогічно можна утворити 48 чотирицифрових чисел з цифр 0, 2, 3, 4, 5, 6, у яких остання цифра 5,
а значить кількість парних чотирицифрових чисел, які можна утворити з цифр 0, 2, 3, 4, 5, 6, якщо кожна з цифр не повторюється буде 300-48-48=204
Количество элементарных исходов равно 64, так как по формуле размещений с повторениями 8*8=64. Количество элементарных исходов, благоприятствующих событию, описываемому в задаче равно 8, это число можно получить перебором.
Число делится на 9, если сумма его цифр делится на 9. Сумма цифр двузначного числа, делящегося на 9, может равняться либо 9, либо 18. По условию задачи, цифры меньше 9, значит, сумма цифр не может быть равна 18 (9+9=18). Значит, нужно рассмотреть все двузначные числа, в которых сумма цифр равна 9. Это числа: 18, 27, 36, 45, 54, 63, 72, 81.
Так как нет оснований полагать, что каким-либо цифрам было отдано предпочтение, то есть, вероятность любого числа, написанного на доске, одинакова, то здесь применима формула, называемая классическим определением вероятности, согласно которой вероятность нужного нам события равна отношению количества благоприятствующих событию исходов к общему количеству исходов, то есть, .
204
Объяснение:
Спочатку розглянемо скільки можна утворити чотирицифрових чисел з цифр 0, 2, 3, 4, 5, 6, якщо кожна з цифр не повторюється
(0 не можна ставити на першу позицію), значить варіантів утворити число буде 5*5*4*3=300 (будь яку ненульову цифру на першу позицію, на другу позицію будь-яку з решти 5-ти цифр (уже включаючи 0 для вибору) після вибору першої, на третю будь-яку з решти 4-ох після вибору перших двох, і на четверту позицію відповідно 3 варіанта вибору)
Тепер розглянемо скільки можна утворити чотирицифрових чисел з цифр 0, 2, 3, 4, 5, 6, у яких остання цифра 3:
(0 і 3 не можна ставити на першу позицію, 3 на останній позиції, не можна повторюватися), 4*4*3*1=48
Аналогічно можна утворити 48 чотирицифрових чисел з цифр 0, 2, 3, 4, 5, 6, у яких остання цифра 5,
а значить кількість парних чотирицифрових чисел, які можна утворити з цифр 0, 2, 3, 4, 5, 6, якщо кожна з цифр не повторюється буде 300-48-48=204
ответ: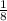
Объяснение:
Количество элементарных исходов равно 64, так как по формуле размещений с повторениями 8*8=64. Количество элементарных исходов, благоприятствующих событию, описываемому в задаче равно 8, это число можно получить перебором.
Число делится на 9, если сумма его цифр делится на 9. Сумма цифр двузначного числа, делящегося на 9, может равняться либо 9, либо 18. По условию задачи, цифры меньше 9, значит, сумма цифр не может быть равна 18 (9+9=18). Значит, нужно рассмотреть все двузначные числа, в которых сумма цифр равна 9. Это числа: 18, 27, 36, 45, 54, 63, 72, 81.
Так как нет оснований полагать, что каким-либо цифрам было отдано предпочтение, то есть, вероятность любого числа, написанного на доске, одинакова, то здесь применима формула, называемая классическим определением вероятности, согласно которой вероятность нужного нам события равна отношению количества благоприятствующих событию исходов к общему количеству исходов, то есть,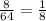 .
.