1. Всего пятизначных чисел: 9*10*10*10*10 = 90000. Количество пятизначных чисел, в которых первая цифра - пятерка, равно: 4*9*9*9 = 2916 (Одна из оставшихся цифр - пятерка, поэтому можно варьировать только 3 разряда, причем цифрами от 0 до 4 и от 6 до 9 - отсюда три множителя 9. Пятерка может быть любым из четырех оставшихся разрядов - отсюда множитель 4). Количество пятизначных чисел, в которых первая цифра - не пятерка, равно: 8*6*9*9 = 3888 (Первую цифру можно выбрать это не 0 и не 5. Из оставшихся четырех цифр можно варьировать 2 разряда, причем цифрами от 0 до 4 и от 6 до 9 - отсюда два множителя 9. Две пятерки могут располагаться на четырех местах отсюда множитель 6). Искомая вероятность равна: (2916+3888)/90000 = 0,0756.
2. Всего шестизначных чисел: 9*10*10*10*10*10 = 900000. Количество шестизначных чисел, у которых первая цифра - семерка, равно: 10*9*9*9 = 7290 (Две оставшихся цифры - семерки, поэтому варьировать можно только три разряда, причем цифрами от 0 до 6 и от 8 до 9 - отсюда три множителя 9. Две семерки могут располагаться на пяти местах отсюда множитель 10). Количество шестизначных чисел, у которых первая цифра - не семерка, равно: 8*10*9*9 = 6480 (Первую цифру можно выбрать это не 0 и не 7. Из оставшихся пяти разрядов варьировать можно 2, причем цифрами от 0 до 6 и от 8 до 9 - отсюда два множителя 9. Две семерки могут располагаться на пяти местах отсюда множитель 10). Искомая вероятность равна: (7290+6480)/900000 = 0,0153.
Степенью числа a > 0 с рациональным показателем является степень, показатель которой представим в виде обыкновенной несократимой дроби x = m/n, где m целое, а n натуральное число, причём n > 1 (x - показатель степени).
Свойства степеней с рациональным показателем:
1.) Для любого положительного a и любого рационального x, число - положительно.
2.) При a < 0 рациональная степень числа a не определяется. (Так как подкоренное выражение не может быть меньше или равняться нулю, что свойственно для множества действительных чисел, во множестве же комплексных чисел данное правило не действует)
3.) Любое рациональная степень может записываться в различных формах, например md/nd( при любом натуральном d), значение , в свою очередь, не зависит от форм записи x.
Степень с рациональным показателем также унаследует все свойства степеней с натуральным показателем, разумеется при положительном a.
2.) Квадратным трёхчленом называется многочлен вида + вх + с, где a,b,c - числа, x - переменная, причём a не равно нулю.
Формула разложения квадратного трёхчлена представляется в виде:
(ax - ax1)(x- x2), выведем данную формулу.
+ вх + с
Вынесем a за скобки, тогда получим:
a( + в/aх + с/a).
Из теоремы Виета для квадратичной функции известно, что
x1*x2 = c/a
x1 + x2 = -b/a. Здесь и далее x1 и x2 - корни квадратного уравнения + вх + с = 0.
1.) Два угла одного треугольника соответственно равны двум углам другого треугольника. (Подобие по двум углам)
2.) Две стороны одного треугольника, соответственно пропорциональны двум сторонам другого, при условии, что углы между сторонами равны.(Подобие по двум сторонам и углу).
3.) Три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника.
Признаки подобия прямоугольных треугольников:
1.) Если острый угол одного прямоугольного треугольника соответственно равен острому углу другого прямоугольного треугольника. (Подобие по острому углу).
2.) Если два катета одного прямоугольного треугольника соответственно пропорциональны двум катетам другого прямоугольного треугольника. (Подобие по двум катетам)
3.) Если катет и гипотенуза одного прямоугольного треугольника соответственно пропорциональны катету и гипотенузе другого прямоугольного треугольника.
9*10*10*10*10 = 90000.
Количество пятизначных чисел, в которых первая цифра - пятерка, равно:
4*9*9*9 = 2916 (Одна из оставшихся цифр - пятерка, поэтому можно варьировать только 3 разряда, причем цифрами от 0 до 4 и от 6 до 9 - отсюда три множителя 9. Пятерка может быть любым из четырех оставшихся разрядов - отсюда множитель 4).
Количество пятизначных чисел, в которых первая цифра - не пятерка, равно:
8*6*9*9 = 3888 (Первую цифру можно выбрать это не 0 и не 5. Из оставшихся четырех цифр можно варьировать 2 разряда, причем цифрами от 0 до 4 и от 6 до 9 - отсюда два множителя 9. Две пятерки могут располагаться на четырех местах отсюда множитель 6).
Искомая вероятность равна:
(2916+3888)/90000 = 0,0756.
2. Всего шестизначных чисел:
9*10*10*10*10*10 = 900000.
Количество шестизначных чисел, у которых первая цифра - семерка, равно:
10*9*9*9 = 7290 (Две оставшихся цифры - семерки, поэтому варьировать можно только три разряда, причем цифрами от 0 до 6 и от 8 до 9 - отсюда три множителя 9. Две семерки могут располагаться на пяти местах отсюда множитель 10).
Количество шестизначных чисел, у которых первая цифра - не семерка, равно:
8*10*9*9 = 6480 (Первую цифру можно выбрать это не 0 и не 7. Из оставшихся пяти разрядов варьировать можно 2, причем цифрами от 0 до 6 и от 8 до 9 - отсюда два множителя 9. Две семерки могут располагаться на пяти местах отсюда множитель 10).
Искомая вероятность равна:
(7290+6480)/900000 = 0,0153.
Степенью числа a > 0 с рациональным показателем является степень, показатель которой представим в виде обыкновенной несократимой дроби x = m/n, где m целое, а n натуральное число, причём n > 1 (x - показатель степени).
Свойства степеней с рациональным показателем:
1.) Для любого положительного a и любого рационального x, число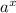
- положительно.
2.) При a < 0 рациональная степень числа a не определяется. (Так как подкоренное выражение не может быть меньше или равняться нулю, что свойственно для множества действительных чисел, во множестве же комплексных чисел данное правило не действует)
3.) Любое рациональная степень может записываться в различных формах, например md/nd( при любом натуральном d), значение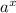
, в свою очередь, не зависит от форм записи x.
Степень с рациональным показателем также унаследует все свойства степеней с натуральным показателем, разумеется при положительном a.
2.) Квадратным трёхчленом называется многочлен вида
+ вх + с, где a,b,c - числа, x - переменная, причём a не равно нулю.
Формула разложения квадратного трёхчлена представляется в виде:
(ax - ax1)(x- x2), выведем данную формулу.
Вынесем a за скобки, тогда получим:
a(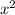
+ в/aх + с/a).
Из теоремы Виета для квадратичной функции известно, что
x1*x2 = c/a
x1 + x2 = -b/a. Здесь и далее x1 и x2 - корни квадратного уравнения
+ вх + с = 0.
Преобразуем в соответствиии с теоремой Виета:
a(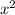
- (x1 + x2)х + x1x2) =>
=> a((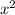
- xx1) - (x2x - x1x2)) = >
=> a(х (х — x1) — x2(х — x1)) = > a(x - x1)(x - x2) =>
=> (ax - ax1)(x - x2).
Признаки подобия треугольников:
1.) Два угла одного треугольника соответственно равны двум углам другого треугольника. (Подобие по двум углам)
2.) Две стороны одного треугольника, соответственно пропорциональны двум сторонам другого, при условии, что углы между сторонами равны.(Подобие по двум сторонам и углу).
3.) Три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника.
Признаки подобия прямоугольных треугольников:
1.) Если острый угол одного прямоугольного треугольника соответственно равен острому углу другого прямоугольного треугольника. (Подобие по острому углу).
2.) Если два катета одного прямоугольного треугольника соответственно пропорциональны двум катетам другого прямоугольного треугольника. (Подобие по двум катетам)
3.) Если катет и гипотенуза одного прямоугольного треугольника соответственно пропорциональны катету и гипотенузе другого прямоугольного треугольника.
Ух...замучился я...