Расстояние от путника до башни составляет:
0,002 · 1000 = 2 метра,
где 1000 - количество метров в одном километре.
2) Так как диаметр башни равен 60 дм = 6 м (в одном метре 10 дециметров) , то расстояние от путника до центра башни составляет:
2 + 3 = 5 метров, где 3 метра - это радиус башни.
3) Арбалетчик находится на расстоянии 3 м от центра башни, т.к. движется по окружности, диаметр которой равен 6 м.
4) Если провести линию между путником и арбалетчиком, то она будет касательной к окружности, по которой движется арбалетчик.
Касательная перпендикулярна радиусу и её можно найти по теореме Пифагора:
х (расстояние до путника) = √(5² - 3²) = √(25-9) = √16 = 4 м
ответ: путник находится на расстоянии 4 м от арбалетчика
№1
а) 3х²=12х
3х²-12х=0
х(3х-12)=0
х₁=0; х₂=4.
ответ: х₁=0; х₂=4.
б) х⁴-2х²=8
(х²)²-2х²-8=0
Пусть х²=t, тогда
t²-2t-8=0
D=(-2)²-4*1*(-8)=36
t₁=== 2
t₂=== -4
Вернёмся к уравнению:
1) х²=2 2)х²= -4
х₁=; х₂= х - не имеет ответа.
ответ: х₁=; х₂= .
в) (х²-16)(х²+2х-8)=0
1) х²-16=0 2) х²+2х-8=0
х²=16 D=(-2)²-4*1*(-8)=36
х₁=4; х₂= -4. х₃===2
х₄=== -4
ответ: х₁=4; х₂=х₄= -4; х₃=2
г) =0
2х²-3х-5=0
D=(-3)²-4*2*(-5)=49
х₁===2,5
х₂=== -1
ОДЗ (обще-допустимые значения):
х - не равно 2,5 т.к 2*2,5-5=0, а на ноль делить нельзя.
х= -1.
ответ: х= -1
№2
Пусть x - первое число, тогда х-8 - второе число. Произведение этих чисел равно 105. Составим уравнение:
х*(х-8)=105
х²-8х-105=0
D=(-8)²-4*1*(-105)=484
х₁===15
х₂=== -7
ответ: 15 наибольшее число.
Расстояние от путника до башни составляет:
0,002 · 1000 = 2 метра,
где 1000 - количество метров в одном километре.
2) Так как диаметр башни равен 60 дм = 6 м (в одном метре 10 дециметров) , то расстояние от путника до центра башни составляет:
2 + 3 = 5 метров, где 3 метра - это радиус башни.
3) Арбалетчик находится на расстоянии 3 м от центра башни, т.к. движется по окружности, диаметр которой равен 6 м.
4) Если провести линию между путником и арбалетчиком, то она будет касательной к окружности, по которой движется арбалетчик.
Касательная перпендикулярна радиусу и её можно найти по теореме Пифагора:
х (расстояние до путника) = √(5² - 3²) = √(25-9) = √16 = 4 м
ответ: путник находится на расстоянии 4 м от арбалетчика
№1
а) 3х²=12х
3х²-12х=0
х(3х-12)=0
х₁=0; х₂=4.
ответ: х₁=0; х₂=4.
б) х⁴-2х²=8
(х²)²-2х²-8=0
Пусть х²=t, тогда
t²-2t-8=0
D=(-2)²-4*1*(-8)=36
t₁=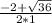 =
=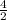 = 2
= 2
t₂=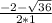 =
=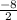 = -4
= -4
Вернёмся к уравнению:
1) х²=2 2)х²= -4
х₁=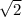 ; х₂=
; х₂=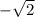 х - не имеет ответа.
х - не имеет ответа.
ответ: х₁=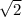 ; х₂=
; х₂=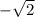 .
.
в) (х²-16)(х²+2х-8)=0
1) х²-16=0 2) х²+2х-8=0
х²=16 D=(-2)²-4*1*(-8)=36
х₁=4; х₂= -4. х₃=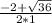 =
=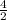 =2
=2
х₄=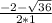 =
=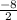 = -4
= -4
ответ: х₁=4; х₂=х₄= -4; х₃=2
г)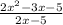 =0
=0
2х²-3х-5=0
D=(-3)²-4*2*(-5)=49
х₁=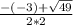 =
=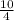 =2,5
=2,5
х₂=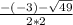 =
=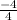 = -1
= -1
ОДЗ (обще-допустимые значения):
х - не равно 2,5 т.к 2*2,5-5=0, а на ноль делить нельзя.
х= -1.
ответ: х= -1
№2
Пусть x - первое число, тогда х-8 - второе число. Произведение этих чисел равно 105. Составим уравнение:
х*(х-8)=105
х²-8х-105=0
D=(-8)²-4*1*(-105)=484
х₁=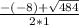 =
=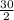 =15
=15
х₂=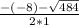 =
=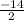 = -7
= -7
ответ: 15 наибольшее число.