Исследуем функцию, заданную формулой:
Область определения:
Данная функция определена для:
ответ: .
Первая производная:
====
Вторая производная:
Вторая производная это производная от первой производной.
==
Точки пересечения с осью :
Для нахождения точек пересечения с осью абсцисс приравняем функцию к нулю.
Дробь обращается в нуль тогда, когда числитель равен нулю.
Пусть
Вертикальные асимптоты:
Определим значения аргумента, при которых знаменатель функции обращается в ноль
Наклонные асимптоты: .
Предел разности исходной функции и функции на бесконечности равен нулю.
Критические точки:
Случай .
Возможные точки перегиба: нет
Для нахождения возможных точек перегиба приравняем вторую производную к нулю и решим полученное уравнение.
ответ: нет решений.
Функция f(x) называется четной, если f(-x)=f(x).
=====
Симметрия относительно начала координат: нет
Функция f(x) называется нечетной, если f(-x)=-f(x).
=
Относительные экстремумы:
Проходя через точку минимума, производная функции меняет знак с (-) на (+).
Относительный минимум .
Проходя через точку максимума. производная функции меняет знак с (+) на (-).
Относительный максимум .
отметь мой ответ лучшим) нужно что бы стать умным:))
чтобы найти наименьшее значение функции, нужно сначала найти ее производную
(производная от cosx = -sinx и еще надо не забыть множитель 2)
далее нужно найти стационарные точки
это те точки, в которых производная равна нулю
следовательно приравняем нашу производную к нулю
т.к. синус не может принимать значения меньше -1, то стационарных точек нет и функция всегда возрастает или убывает
именно это мы сейчас и узнаем
для этого нужно понять, положительна ли производная или отрицательна
-2sinx имеет максимальное значение равное 2 (если синус будет равен -1, то (-2)*(-1)=2)
2-11<0, следовательно производная отрицательна и функция всегда убывает
нам нужно найти наименьшее значение на определенном промежутке [-;0]
поскольку мы выяснили, что наша функция всегда убывает, то наименьшее значение будет при наибольшем х
в нашем случае на промежутке [-;0] набольший х=0
и нам остается только лишь посчитать значение функции в нуле
ответ: y наименьшее = 9
Исследуем функцию, заданную формулой:
Область определения:
Данная функция определена для:
ответ: .
Первая производная:
====
====
Вторая производная:
Вторая производная это производная от первой производной.
==
==
==
==
==
==
==
==
====
Точки пересечения с осью :
Для нахождения точек пересечения с осью абсцисс приравняем функцию к нулю.
Дробь обращается в нуль тогда, когда числитель равен нулю.
ответ: .
Точки пересечения с осью :
Пусть
Вертикальные асимптоты:
Определим значения аргумента, при которых знаменатель функции обращается в ноль
Наклонные асимптоты: .
==
Предел разности исходной функции и функции на бесконечности равен нулю.
Критические точки:
Случай .
Случай .
ответ: .
Возможные точки перегиба: нет
Для нахождения возможных точек перегиба приравняем вторую производную к нулю и решим полученное уравнение.
ответ: нет решений.
Функция f(x) называется четной, если f(-x)=f(x).
=====
=====
Симметрия относительно начала координат: нет
Функция f(x) называется нечетной, если f(-x)=-f(x).
=
=====
====
==
Относительные экстремумы:
Проходя через точку минимума, производная функции меняет знак с (-) на (+).
Относительный минимум .
Проходя через точку максимума. производная функции меняет знак с (+) на (-).
Относительный максимум .
отметь мой ответ лучшим) нужно что бы стать умным:))
чтобы найти наименьшее значение функции, нужно сначала найти ее производную
далее нужно найти стационарные точки
это те точки, в которых производная равна нулю
следовательно приравняем нашу производную к нулю
именно это мы сейчас и узнаем
для этого нужно понять, положительна ли производная или отрицательна
-2sinx имеет максимальное значение равное 2 (если синус будет равен -1, то (-2)*(-1)=2)
2-11<0, следовательно производная отрицательна и функция всегда убывает
нам нужно найти наименьшее значение на определенном промежутке [-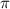
;0]
поскольку мы выяснили, что наша функция всегда убывает, то наименьшее значение будет при наибольшем х
в нашем случае на промежутке [-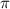
;0] набольший х=0
и нам остается только лишь посчитать значение функции в нуле
ответ: y наименьшее = 9