1. Область определения функции: множество всех действительных чисел
2. Чётность и нечётность функции: проверим на четность функции с соотношений:
Итак, f(-x) = f(x) значит заданная функция является четной.
3. Точки пересечения с осями координат.
3.1. точки пересечения с осью Ох. График функции пересекает ось абсциссу при f = 0 значит нужно решить уравнение:
(0;0), (2;0), (-2;0) - точки.
3.2. точки пересечения с осью Оу. График пересекает ось ординат, когда х=0, т.е. подставляем x=0 в функцию, получим
(0;0) - точка
4. Функция не является периодичной.
5. Экстремумы функции
Для того, чтобы найти экстремумы, нужно решить уравнение
Найдем интервалы возрастание и убывания функции:
______+____(-√2)_____-____(0)________+_____(√2)______-____
Функция возрастает на промежутке , а убывает -
- локальные максимумы
- локальный минимум.
6. Точки перегиба.
Вторая производная функции:
___-____(-√6/3)____+__(√6/3)___-____
Функция вогнутая на промежутке , а выпуклая на промежутке
7. Асимптоты
Здесь вертикальных асимптот нет. Найдем теперь горизонтальные асимптоты.
Горизонтальные асимптоты найдём с пределов данной функции при
Предел не существует, следовательно горизонтальной асимптоты нет.
Вертикальной асимптоты нет.
Solution :
{x,y} = {24,26}
System of Linear Equations entered :
[1] x - 2y = -28 [2] x - y = -2
Graphic Representation of the Equations :
-2y + x = -28 y + x = -2
olve by Substitution :
// Solve equation [2] for the variable x
[2] x = y - 2
// Plug this in for variable x in equation [1]
[1] (y -2) - 2y = -28 [1] - y = -26
// Solve equation [1] for the variable y
[1] y = 26
// By now we know this much :
x = y-2 y = 26
// Use the y value to solve for x
x = (26)-2 = 24
Solution :
{x,y} = {24,26}
1. Область определения функции: множество всех действительных чисел
2. Чётность и нечётность функции: проверим на четность функции с соотношений: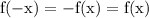
Итак, f(-x) = f(x) значит заданная функция является четной.
3. Точки пересечения с осями координат.
3.1. точки пересечения с осью Ох. График функции пересекает ось абсциссу при f = 0 значит нужно решить уравнение:
(0;0), (2;0), (-2;0) - точки.
3.2. точки пересечения с осью Оу. График пересекает ось ординат, когда х=0, т.е. подставляем x=0 в функцию, получим
(0;0) - точка
4. Функция не является периодичной.
5. Экстремумы функции
Для того, чтобы найти экстремумы, нужно решить уравнение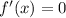
Найдем интервалы возрастание и убывания функции:
______+____(-√2)_____-____(0)________+_____(√2)______-____
Функция возрастает на промежутке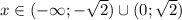 , а убывает -
, а убывает - 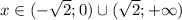
6. Точки перегиба.
Вторая производная функции: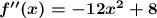
___-____(-√6/3)____+__(√6/3)___-____
Функция вогнутая на промежутке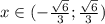 , а выпуклая на промежутке
, а выпуклая на промежутке 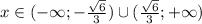
7. Асимптоты
Здесь вертикальных асимптот нет. Найдем теперь горизонтальные асимптоты.
Горизонтальные асимптоты найдём с пределов данной функции при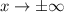
Предел не существует, следовательно горизонтальной асимптоты нет.
Вертикальной асимптоты нет.