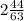1/cos x + 1/sin x = -2√2 (sin x + cos x)/(sin x*cos x) = -2√2 sin x + cos x = -2√2*sin x*cos x Есть такое равенство: sin x + cos x = √2*sin(x + pi/4) Доказать его очень просто, разложив синус суммы справа. √2*sin(x + pi/4) = √2*(sin x*cos pi/4 + cos x*sin pi/4) = = √2*(sin x*1/√2 + cos x*1/√2) = sin x + cos x √2sin(x + pi/4) = -√2*sin 2x sin(x + pi/4) = -sin 2x sin(x + pi/4) + sin 2x = 0 Раскладываем сумму синусов Упрощаем и делим на 2 Если произведение равно 0, то один из множителей равен 0.
(sin x + cos x)/(sin x*cos x) = -2√2
sin x + cos x = -2√2*sin x*cos x
Есть такое равенство: sin x + cos x = √2*sin(x + pi/4)
Доказать его очень просто, разложив синус суммы справа.
√2*sin(x + pi/4) = √2*(sin x*cos pi/4 + cos x*sin pi/4) =
= √2*(sin x*1/√2 + cos x*1/√2) = sin x + cos x
√2sin(x + pi/4) = -√2*sin 2x
sin(x + pi/4) = -sin 2x
sin(x + pi/4) + sin 2x = 0
Раскладываем сумму синусов
Упрощаем и делим на 2
Если произведение равно 0, то один из множителей равен 0.
1)
(12x + pi)/8 = pi*k
12x = -pi + 8pi*k
x1 = -pi/12 + 8pi/12*k = -pi/12 + 2pi/3*k
2)
4x - pi = pi/2 + pi*n
4x = pi/2 + pi + pi*n = 3pi/2 + pi*n
x2 = 3pi/8 + pi/4*n
Интересное уравнение.
{9x+7y= 5. 11/63
{4x+3y = 2
║
∨
{9x+7y = 326/63;
{4x+3y = 2
Умножим обе части первого уравнения на 63 и получим cистему:
{567x+441y = 326;
{4x+3y = 2 |× (-147)
Умножим обе части второго уравнения на (-147) и получим систему:
{567x+441y = 326;
{-588x -441y = -294
Сложим эти уравнения и получим:
567х+441у-588х-441у=326-294
-21х = 32
х= - 32/21
Подставим х = - 32/21 во второе уравнение 4х + 3у = 2.
4*(-32/21)+3y = 2
3у= 2+128/21
3у = 42/21+128/21
3у =170/21
у = 170/63
Проверка
9*(-32/21) + 7 * 170/63=-864/63+1190/63=326/63=5 11/63
4*(-32/21) +3*(170/63) = -384/63+510/63= 2
Равенства верны.
ответ: x=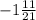 ; y=
; y=