Имеется два сплава,содержащих никель различной концентрации.

Разложите на множителе трехчлен  ₁  ₂

1)  x² - 2x + 12  ;

2) x ² + x + 20 .

Объяснение:    i²  =  -1

1)  x ² - 2x + 12   D₁ = D/4 = (-2/2)² - 12 = (-1)² -12 = -11  < 0 значит  корни квадратного  трехчлена комплексные. [ i = √ (-1) → мнимая единица ]    

x₁ = 1 -√11 i, x₂ = 1 +i√11 i  

* * *x₁+x₂ =2 ; x₁*x₂=( 1 -√11 i)(1 +√11 i) =1² -(11 i)²=1-11i²=1-11*(-1) =1+11 =12 * * *

x²- 2x + 12 = (x -x₁)*(x-x₂) =(x - 1 -(√11) i )*(x - 1 +(√11) i )

z = a+bi  ;   |z|  =r = √(a²+b²)  → модуль комплексного числа  

a =r(cosφ+ i*sinφ)   φ _ аргумент комплексного числа    tgφ =b/a

1) x²-2x+1 ≥ 0

x²-2x+1 = 0

a = 1 , b = -2, c = 1

D = b²-4ac ; D = (-2)² - 4*1*1 = 4-4 = 0 ⇒ у уравнения один корень

;

(x-1)² = 0

Точка будет закрашена, т.к. уравнение нестрогое

       -              +

-------------·--------------->

              1

ответ: х∈[1;+∞)

2) x²-5 < 4х

x²-4х -5 < 0

x²-4х -5 = 0

a = 1 , b = -4, c = -5

D = b²-4ac ; D = (-4)² - 4*1*(-5) = 16+20 = 36 = 6² ⇒ у уравнения два корня

;

;

(x-5)(х+1) = 0

Точки не будут закрашены, т.к. уравнение строгое

    +          -           +              

--------₀----------₀---------->

        -1           5

ответ: х∈(-1;5)

3) x²+4 < х

x²-х+4 < 0

x²-х+4 = 0

a = 1 , b = -1, c = 4

D = b²-4ac ; D = (-1)² - 4*1*4 = 1-16 = -15 ⇒ у уравнения нет корней

ответ: х∉R

4) 6x²+x-1 > 0

6x²+x-1 = 0

a = 6 , b = 1, c = -1

D = b²-4ac ; D = 1² - 4*6*(-1) = 1+24 = 25 = 5² ⇒ у уравнения два корня

;

;

Точки не будут закрашены, т.к. уравнение строгое

    +          -           +              

--------₀----------₀---------->

ответ: х∈(-∞;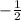)∪(;+∞)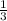