Имеются два сосуда. первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. если эти растворы смешать, то получится раствор, содержащий 80% кислоты. если же смешать равные массы этих растворов, то получится раствор, содержащий 83% кислоты. сколько килограммов кислоты содержится в первом сосуде?
ответ: 20.4 кг.
Объяснение:
пусть в 1) сосуде (х) кг кислоты; во 2) (у) кг кислоты;
тогда по условию х+у = 0.8*50
(30кг+20кг=50кг; 80% от числа находим, умножая на 80/100)
х+у = 40 ---> y = 40-x
возьмем равные массы растворов (например, по 1 кг)
1)
в 30 кг ---> x кг кислоты
в 1 кг ---> (x/30) кг кислоты
2)
в 20 кг ---> (40-x) кг кислоты
в 1 кг ---> (40-х)/20 кг кислоты
получим второе уравнение: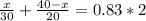
(1кг+1кг=2кг; 83% от числа находим, умножая на 83/100)
умножим обе части равенства на 60 (чтобы вычислять без дробей)
2х + 120 - 3х = 99.6
х = 20.4
и можно проверить:
20.4 + 40 - 20.4 = 8*5 (очевидно)
1) в 1 кг раствора содержится 20.4/30 = 204/300 = 68/100 кг кислоты
2) в 1 кг раствора содержится 19.6/20 = 196/200 = 98/100 кг кислоты
если смешать, получится (68+98)/100 = 166/100
это =2*0.83