(см. объяснение)
Объяснение:
По условию мы не знаем, что перед нами парабола.
Итак видим неизвестный науке объект:
Найдем область определения функции:
Учитывая, что функция непрерывна, найдем множество значений:
Тогда .
Функция не является ни четной, ни нечетной.
Определим промежутки возрастания/убывания функции:
Тогда функция убывает до , а затем возрастает.
Определим выпуклость функции:
Следовательно функция выпукла вниз.
Составим таблицу для некоторых точек функции:
x|-2|-1|1 |3|4
y|5 |0|-4|0|5
Построим эскиз функции (см. прикрепленный файл).
Получилось какое-то коническое сечение с единичным эксцентриситетом.
Задание выполнено!
3a^2+5ab=19+2b^2
a, b > 0 a,b ∈ N
разложим 3a^2+5ab=2b^2
3a^2+5ab -2b^2 = 0
D = (5b)^2 + 4*3*2b^2 = 25b^2 + 24b^2 = 49b^2
a12 = (-5b +- 7b)/6 = -2b 1/3b
3a^2+5ab -2b^2 = (a - 1/3b)(a + 2b) = (3a - b)(a + 2b)
получили
(3a - b)(a + 2b) = 19
19 простое делится на +- 1 и +- 19
значит и множители могут быть только целыми в левой части
19 = 1*19 = (-1) * (-19)
получаем системы
1. 3a - b = -1
a + 2b = -19 нет a, b > 0
2. 3a - b = -19
a + 2b = -1 нет a, b > 0
3. 3a - b = 1
a + 2b = 19
4. 3a - b = 19
a + 2b = 1 нет a, b > 0
решаем только одну систему
3a - b = 1
--
b = 3a - 1
a + 2(3a - 1) = 19
a + 6a -2 = 19
7a = 21
a = 3
b = 3a - 1 = 3*3 - 1 = 8
ответ (3, 8)
(см. объяснение)
Объяснение:
По условию мы не знаем, что перед нами парабола.
Итак видим неизвестный науке объект:
Найдем область определения функции:
Учитывая, что функция непрерывна, найдем множество значений:
Тогда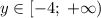 .
.
Функция не является ни четной, ни нечетной.
Определим промежутки возрастания/убывания функции:
Тогда функция убывает до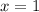 , а затем возрастает.
, а затем возрастает.
Определим выпуклость функции:
Следовательно функция выпукла вниз.
Составим таблицу для некоторых точек функции:
x|-2|-1|1 |3|4
y|5 |0|-4|0|5
Построим эскиз функции (см. прикрепленный файл).
Получилось какое-то коническое сечение с единичным эксцентриситетом.
Задание выполнено!
3a^2+5ab=19+2b^2
a, b > 0 a,b ∈ N
разложим 3a^2+5ab=2b^2
3a^2+5ab -2b^2 = 0
D = (5b)^2 + 4*3*2b^2 = 25b^2 + 24b^2 = 49b^2
a12 = (-5b +- 7b)/6 = -2b 1/3b
3a^2+5ab -2b^2 = (a - 1/3b)(a + 2b) = (3a - b)(a + 2b)
получили
(3a - b)(a + 2b) = 19
19 простое делится на +- 1 и +- 19
значит и множители могут быть только целыми в левой части
19 = 1*19 = (-1) * (-19)
получаем системы
1. 3a - b = -1
a + 2b = -19 нет a, b > 0
2. 3a - b = -19
a + 2b = -1 нет a, b > 0
3. 3a - b = 1
a + 2b = 19
4. 3a - b = 19
a + 2b = 1 нет a, b > 0
решаем только одну систему
3a - b = 1
a + 2b = 19
--
b = 3a - 1
a + 2(3a - 1) = 19
a + 6a -2 = 19
7a = 21
a = 3
b = 3a - 1 = 3*3 - 1 = 8
ответ (3, 8)