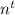Пусть известно число , оценим . Тогда достаточно выкинуть из всевозможных слов длины слова, начинающиеся со слов длины (таковых ), то есть . Отсюда , поскольку очевидно, что , ведь максимальное число слов длины есть число
Пусть известно число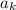 , оценим
, оценим 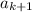 . Тогда достаточно выкинуть из всевозможных слов длины
. Тогда достаточно выкинуть из всевозможных слов длины 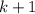 слова, начинающиеся со слов длины
слова, начинающиеся со слов длины 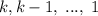 (таковых
(таковых 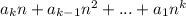 ), то есть
), то есть 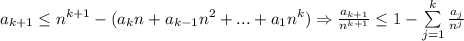 . Отсюда
. Отсюда 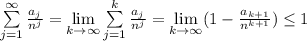 , поскольку очевидно, что
, поскольку очевидно, что 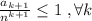 , ведь максимальное число слов длины
, ведь максимальное число слов длины 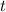 есть число
есть число