1) если x-2 < 0, а подкоренное выражение неотрицательно, то неравенство верно при всех таких х, потому что арифметический квадратный корень при условии его существования всегда неторицателен и значит всегда больше отрицательного выражения справа
⇒ о т в ет 1)
2)если x-2 ≥ 0
Возводим обе части неравенство в квадрат:
О т в е т. 2)
Объединяем ответы первого и второго случаев:
1) если x-2 < 0, а подкоренное выражение неотрицательно, то неравенство верно при всех таких х, потому что арифметический квадратный корень при условии его существования всегда неторицателен и значит всегда больше отрицательного выражения справа
2)если x-2 ≥ 0
Возводим обе части неравенство в квадрат:
О т в е т. 2)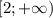
Объединяем ответы первого и второго случаев: