Алгебра: Иррациональные уравнения. система,

Иррациональные уравнения. система
,

Показать ответ

Ответ:

ttleuberlin

28.01.2021 01:26

Ну приступим :)

Из условия задачи, нам известно, что на преодаление пути оба автомобиля потратили одинаковое время, то есть приехали одновременно. Вот от этого и будем отталкиваться. Что нам нужно сделать чтоб узнать время??? Правильно! Расстояние разделить на скорость: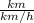 $\frac{km}{km/h}$

Путь расстояние у нас будет едыныця :) 1. Тогда, время потраченное первым авто будет 1/х, а время второго авто будет равно: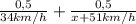 $\frac{0,5}{34km/h}+\frac{0,5}{x+51km/h}$

Как вы наверное догадались, 0,5 это пол пути, ну а "х" это скорость первого авто. Получается:

$\frac{1}{x}-(\frac{0,5}{34}+\frac{0,5}{x+51})=0$

ОДЗ

$x \neq 0 \\x 0$

$\frac{1}{x}-(\frac{1}{68}+\frac{1}{2(x+51)})=0 \\ \\\frac{68(x+51)}{68x(x+51)}-\frac{x(x+51)}{68x(x+51)}-\frac{34x}{2(x+51)34x}=0 \\ \\\frac{68(x+51)-x(x+51)-34x}{68x(x+51)}=0 \\ \\\frac{(68x+3468)-(x^2+51x)-34x}{68x(x+51)}=0 \\ \\\frac{-x^2-17x+3468}{68x(x+51)}=0 \\ \\\frac{x^2+17x-3468}{68x(x+51)}=0$

Произведение равно нулю, если числитель равен нулю:

$x^2+17x-3468=0 \\ \\D=17^2-4*1*(-3468)=14161 \\ \\x_1=\frac{-17-119}{2}=-68$

не удовлетваряет ОДЗ

$x_2=\frac{-17+119}{2}=51$

удовлетворяет ОДЗ

ответ: скорость первого автомобиля равна 51км/ч

0,0(0 оценок)

Ответ:

tatarincevai

28.01.2021 01:26

1. Количество трехзначных чисел, составленных из трех различных цифр из множества цифр 1, 2, 3, 4, 5, 6 и 7, равно количеству размещений без повторения 7 элементов по 3 позициям:

A(7, 3) = 7!/(7 - 3)! = 7!/4! = 7 * 6 * 5 = 210.

2. В общей формуле A(n, m) = n!/(n - m)!, отношение факториалов называется убывающим факториалом. В частном случае, при n = m получим число перестановок n элементов:

A(n, n) = n!/(n - n)! = n!/0! = n!

3. Аналогичный результат получим для размещений n элементов по (n - 1) позициям:

A(n, n - 1) = n!/(n - n + 1)! = n!/1! = n!

ответ. Количество трехзначных чисел: 210

Объяснение:

0,0(0 оценок)

Популярные вопросы: Алгебра