Знайдемо другий член, використовуючи формулу суми членів арифметичної прогресії:
Знайдемо різницю арифметичної прогресії, використовуючи ту властивість геометричної прогресії, що її член є середнім геометричних двох сусідніх членів:
Розв'яжемо останнє рівняння через дискримінант:
Тепер перевіримо, чи задовольняють ці корені умові. Перший випадок:
Усі корені (2, 4, 6) додатні, тому задовольняє.
Другий випадок:
У цій прогресії (11, 4, –3) один з членів від'ємний, а отже, не задовольняє умові.
Объяснение:
Решаем квадратное уравнение под корнем.
Дано: y =1*x²+-4*x+-21 - квадратное уравнение.
Вычисляем дискриминант - D.
D = b² - 4*a*c = -4² - 4*(1)*(-21) = 100 - дискриминант. √D = 10.
Вычисляем корни уравнения.
x₁ = (-b+√D)/(2*a) = (4+10)/(2*1) = 14/2 = 7 - первый корень
x₂ = (-b-√D)/(2*a) = (4-10)/(2*1) = -6/2 = -3 - второй корень
х = 7 и х = -3 - корни уравнения.
Парабола положительна ВНЕ КОРНЕЙ.
(-∞;-3] ∪ [7;+∞) - для радикала.
Не допускается деление на ноль в дроби.
х² ≠ 64, х ≠ ± 8 - для дроби.
Объединяем.
D(y) = (-∞;-8)∪(-8;-3] ∪ [7;8)∪(8;+∞) - ООФ - ответ.
Знайдемо другий член, використовуючи формулу суми членів арифметичної прогресії:
Знайдемо різницю арифметичної прогресії, використовуючи ту властивість геометричної прогресії, що її член є середнім геометричних двох сусідніх членів:
Розв'яжемо останнє рівняння через дискримінант:
Тепер перевіримо, чи задовольняють ці корені умові. Перший випадок:
Усі корені (2, 4, 6) додатні, тому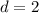 задовольняє.
задовольняє.
Другий випадок:
У цій прогресії (11, 4, –3) один з членів від'ємний, а отже,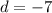 не задовольняє умові.
не задовольняє умові.
Відповідь: 2, 4, 6.