Используя формулы комбинаторики и классическое определение вероятности, решить следующую задачу. Сколько различных комбинаций, состоящих из четырех букв, можно составить из букв: а, в, к, л, о, с ?
2. Используя теоремы сложения и умножения вероятностей, решить следующую задачу.
Студент разыскивает нужную ему формулу в трёх справочниках. Вероятность того, что формула содержится в первом, втором, третьем справочнике, соответственно равны: 0,6; 0,7; 0,8. Найти вероятности того, что формула содержится только в одном справочнике.
3. Используя формулы полной вероятности решить следующую задачу.
В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.
4. Используя формулы Байеса, решить следующую задачу.
Фирма имеет три источника поставки комплектующих – фирмы А, В и С. На долю фирмы А приходится 50% общего объема поставок, В – 30% и С – 20%. Из практики известно, что 10% поставляемых фирмой А деталей бракованные, фирмой В – 5% и фирмой С – 6%. Какова вероятность, что взятая наугад и оказавшаяся бракованной деталь получена от фирмы А?
5. Используя локальную или интегральную теоремы Лапласа, решить следующую задачу.
В каждом из 600 независимых испытаний событие A происходит с постоянной вероятностью 0,65. Найдите вероятность того, что событие A происходит ровно 320 раз
Дана система уравнений :
{х+ Зу = 5, это прямая линия у = (-1/3)х + (5/3)
{х² + y² = 25, это окружность с центром в начале координат и радиусом 5.
Общая схема графического решения - начертить окружность и провести линию через 2 точки: х = 0, у = (5/3) и у = 0, х = 5.
Точки пересечения линий и есть решение.
Можно аналитически проверить его правильность.
{х+ Зу = 5, х = 5 - 3у подставить во второе уравнение.
{х² +y² = 25. (5 - 3у)² + у² = 25.
25 - 30у + 9у² + у² = 25. Решаем квадратное уравнение:
10у² - 30у = 0 или 10у(у - 3) = 0.
Получили 2 корня: у1 = 0 и у2 = 3, отсюда соответствующие координаты по оси Ох равны:
х1 = 5, х2 = -4.
Функция не имеет промежутков убывания
Объяснение:
По теореме если угловой коэффициент прямой меньше нуля, то функция убывает, а если угловой коэффициент прямой больше нуля, то функция возрастает.
Докажем теорему
Рассмотрим функцию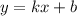
.Где x,y - переменные; k,b - параметры. Продифференцируем функцию y.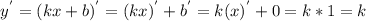
По теореме если производная больше нуля на промежутке M, то на этом промежутке функция возрастает.
По теореме если производная меньше нуля на промежутке M, то на этом промежутке функция убывает.
Тогда согласно теоремам:
если k < 0, то функция убывает.
если k > 0, то функция возрастает.
y=2x − 4 ⇒ k > 0, тогда функция возрастает при x є R.