в данном методе нужно сложить левые части обоих уравнений и приравнять к сумме правых частей:
(5х - 4у) + (7х + 4у) = 22 + 2, 5х - 4у + 7х + 4у = 24 - как видим -4у и +4у сокращаются, так как их сумма равна 0 и получаем упрощенное уравнение, 5х + 7х = 24, 12х = 24, х = 2, теперь из любого из уравнений выделяем у: если из 1 ур-ия: у = (5х - 22) : 4 = (5*2 - 22) : 4 = -3, или если из 2 ур-ия: у = (2 - 7х) : 4 = (2 - 7*2) : 4 = -3 (как видим результат у одинаков).
Объяснение:
х км/ч - скорость катера в стоячей воде;
(x-2) км/ч - скорость катера против течения;
(x+2) км/ч - скорость катера по течению;
20/(x+2) ч - время, пройденное по течению;
8/(x-2) ч - время, пройденное против течения.
На весь путь катер затратил 2 часа, составим уравнение
Домножив обе части уравнения на 0.5(x+2)(x-2), получаем
10(x-2) + 4(x+2) = (x+2)(x-2)
10x - 20 + 4x + 8 = x² - 4
x² - 14x + 8 = 0
D = 14² - 4 * 1 * 8 = 164
Корень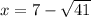
не удовлетворяет условию.
║ 7x+4y=2,
метод сложения:
в данном методе нужно сложить левые части обоих уравнений и приравнять к сумме правых частей:
(5х - 4у) + (7х + 4у) = 22 + 2,
5х - 4у + 7х + 4у = 24 - как видим -4у и +4у сокращаются, так как их сумма равна 0 и получаем упрощенное уравнение,
5х + 7х = 24,
12х = 24,
х = 2,
теперь из любого из уравнений выделяем у:
если из 1 ур-ия: у = (5х - 22) : 4 = (5*2 - 22) : 4 = -3, или
если из 2 ур-ия: у = (2 - 7х) : 4 = (2 - 7*2) : 4 = -3 (как видим результат у одинаков).
ответ: (2; -3)