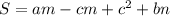Используя свойство факториала n! =n⋅(n−1)⋅(n−2)⋅(n−3)! , сократи данную дробь и результат запиши как произведение чисел, начиная с наибольшего числа. 73/71 значение выражения 23-21/18 равно
Площадь прямоугольника - , где a - длина, b - ширина прямоугольника.
Площадь квадрата - , где a - сторона квадрата.
S - площадь фигуры, всё остальное, отличное от площади фигуры, пишется с индексом рядом с буквой S
1) Чтобы найти площадь первой фигуры, нужно из общей площади сторон вычесть "вырезы"
Sобщая - bc, а выреза - . Вырезы равны, значит и площадь равная, то есть Получаем выражение , что и является ответом.
ответ:
2) Здесь из общей площади надо вычесть обрезанный кусочек, площадь которого (a-b)d, так как a-b - сторона, не данная нам, а следовательно, е' надо записать выражением. Длина нам дана - d.
Sобщая = ac
ответ:
3) Здесь единой стороны, кроме a, не дано вовсе. Чтобы найти ширину, нужно сложить m и n, так как эти числа стоят рядом и, следовательно, в сумме дают общую сторону, которая нам нужна. Но, как видим, нам ну дана противолежащая буквам m, n сторона, а для нахождения площади она является ключевой. Чтобы не усложнять себе жизнь, надо просто из а вычесть с (длина выходящего квадрата) и получить фигуру, площадь которой, при прибавлении площади вывисающего квадрата (его площадь равна по формуле выше), будет общей.
Sобщая =
Теперь, находим площадь оставшегося выреза. Это будет n(a-b-c). Теперь просто подставляем все выражения в одно единое и получаем площадь фигуры
Подготовка к ЕГЭ
Вебинары
Задать вопрос
Войти
АнонимМатематика24 сентября 07:32
Sin3x*cos3x=-1/2 sinx-sin3x+sin5x=0 решите уровнение
ответ или решение1
Стрелков Егор
1. Синус двойного угла:
sin2a = 2sina * cosa;
sin3x * cos3x = -1/2;
2sin3x * cos3x = -1;
sin6x = -1;
6x = -π/2 + 2πk, k ∈ Z;
x = -π/12 + πk/3, k ∈ Z.
2. Сумма синусов:
sina + sinb = 2sin((a + b)/2) * cos((a - b)/2);
sinx - sin3x + sin5x = 0;
(sin5x + sinx) - sin3x = 0;
2sin((5x + x)/2) * cos((5x - x)/2) - sin3x = 0;
2sin3x * cos2x - sin3x = 0;
2sin3x(cos2x - 1/2) = 0;
[sin3x = 0;
[cos2x - 1/2 = 0;
[sin3x = 0;
[cos2x = 1/2;
[3x = πk, k ∈ Z;
[2x = ±π/3 + 2πk, k ∈ Z;
[x = πk/3, k ∈ Z;
[x = ±π/6 + πk, k ∈ Z.
1) -π/12 + πk/3, k ∈ Z;
2) πk/3; ±π/6 + πk, k ∈ Z.
Площадь прямоугольника -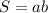
, где a - длина, b - ширина прямоугольника.
Площадь квадрата -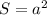
, где a - сторона квадрата.
S - площадь фигуры, всё остальное, отличное от площади фигуры, пишется с индексом рядом с буквой S
1) Чтобы найти площадь первой фигуры, нужно из общей площади сторон вычесть "вырезы"
Sобщая - bc, а выреза -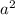
. Вырезы равны, значит и площадь равная, то есть 
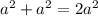Получаем выражение 
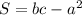, что и является ответом.
ответ: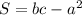
2) Здесь из общей площади надо вычесть обрезанный кусочек, площадь которого (a-b)d, так как a-b - сторона, не данная нам, а следовательно, е' надо записать выражением. Длина нам дана - d.
Sобщая = ac
ответ: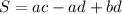
3) Здесь единой стороны, кроме a, не дано вовсе. Чтобы найти ширину, нужно сложить m и n, так как эти числа стоят рядом и, следовательно, в сумме дают общую сторону, которая нам нужна. Но, как видим, нам ну дана противолежащая буквам m, n сторона, а для нахождения площади она является ключевой. Чтобы не усложнять себе жизнь, надо просто из а вычесть с (длина выходящего квадрата) и получить фигуру, площадь которой, при прибавлении площади вывисающего квадрата (его площадь равна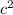
по формуле выше), будет общей.
Sобщая =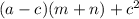
Теперь, находим площадь оставшегося выреза. Это будет n(a-b-c). Теперь просто подставляем все выражения в одно единое и получаем площадь фигуры
ответ: