функция определена на всей действительной оси
Ищем производную
Ищем критические точки
при :
значит т. х=-1 - т.локального минимума, при х є функция убывает
при х є функция возростает
функция определена на всей действительной оси
Ищем производную
Ищем критические точки
при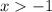 :
: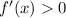
при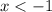 :
: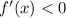
значит т. х=-1 - т.локального минимума, при х є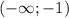 функция убывает
функция убывает
при х є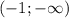 функция возростает
функция возростает