Здесь общий член ряда . Тогда по признаку Коши
По формуле Стирлинга , мы получим
Данный ряд сходится.
Здесь общий член ряда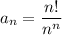 . Тогда по признаку Коши
. Тогда по признаку Коши
По формуле Стирлинга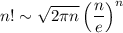 , мы получим
, мы получим
Данный ряд сходится.