Оба знакоположительных ряда ведут себя одинаково, то есть сходятся.
б) Так как ряд , составленный из абсолютных величин сходится, то знакочередующийся ряд сходится абсолютно .
Оба знакоположительных ряда ведут себя одинаково, то есть сходятся.
б) Так как ряд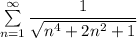 , составленный из абсолютных величин сходится, то знакочередующийся ряд сходится абсолютно .
, составленный из абсолютных величин сходится, то знакочередующийся ряд сходится абсолютно .