Рассмотрим сначала особую точку --- там парабола вырождается в прямую. Тогда
Значит, все дальнейшие рассуждения проводим при .
Найдём корни функции :
где --- вершина параболы и по совместительству точка экстремума функции .
Значение функции в этой точке равно
Из исследования знаков производной/функции легко установить, что при величина --- максимум (это, впрочем, понятно и из вида функции ), больший нуля. Причём в этом случае , т.е. понятно, что в области функция будет падать от какого-то максимального положительного (это в лучшем случае, а может уже и от отрицательного) значения. В любом случае, рано или поздно значение функции станет меньше нуля.
Таким образом, рассматриваем значения .
Ну, раз просят наименьшее целое значение параметра, то не будем далеко ходить и рассмотрим .
Корни и точка экстремума:
Теперь уже - минимум функции, а (после аналогичного анализа) .
Если нам повезёт, то правый (который ) корень будет лежать левее точки , а это будет означать, что к тому времени как функция подойдёт к , она уже будет положительна (ведь правее экстремума парабола рогами вверх будет идти только вверх). Исследуем:
пусть ширина прямоугольника равна x см, тогда длина прямоугольника равна 4x см.
периметр прямоугольника вычисляется по формуле P = 2(a+b), где a и b - стороны прямоугольника. по условию задачи периметр прямоугольника равен 40 см. следовательно:
2(x+4x)=40
2*5x=40
10x=40
x=40/10
x=4 см
значит ширина прямоугольника равна 4 см, а длина прямоугольника равна 4x=4*4=16 см. прямоугольник со сторонами 4 см и 16 см имеет площадь, равную S=ab=4*16=64 см^2.
площадь квадрата вычисляется по формуле S=a^2, где a - сторона квадрата. из формулы площади квадрата можно вывести формулу для нахождения стороны квадрата. если S=a^2, то a=√S. следовательно, квадрат, площадь которого равна площади прямоугольника (то есть 64см^2), будет иметь сторону, равную
Рассмотрим сначала особую точку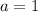 --- там парабола вырождается в прямую. Тогда
--- там парабола вырождается в прямую. Тогда
Значит, все дальнейшие рассуждения проводим при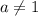 .
.
Найдём корни функции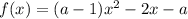 :
:
где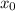 --- вершина параболы и по совместительству точка экстремума функции
--- вершина параболы и по совместительству точка экстремума функции 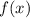 .
.
Значение функции в этой точке равно
Из исследования знаков производной/функции легко установить, что при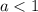 величина
величина 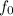 --- максимум (это, впрочем, понятно и из вида функции
--- максимум (это, впрочем, понятно и из вида функции 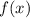 ), больший нуля. Причём в этом случае
), больший нуля. Причём в этом случае  , т.е. понятно, что в области
, т.е. понятно, что в области 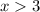 функция будет падать от какого-то максимального положительного (это в лучшем случае, а может уже и от отрицательного) значения. В любом случае, рано или поздно значение функции станет меньше нуля.
функция будет падать от какого-то максимального положительного (это в лучшем случае, а может уже и от отрицательного) значения. В любом случае, рано или поздно значение функции станет меньше нуля.
Таким образом, рассматриваем значения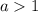 .
.
Ну, раз просят наименьшее целое значение параметра, то не будем далеко ходить и рассмотрим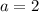 .
.
Корни и точка экстремума:
Теперь уже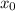 - минимум функции, а (после аналогичного анализа)
- минимум функции, а (после аналогичного анализа) 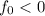 .
.
Если нам повезёт, то правый (который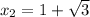 ) корень будет лежать левее точки
) корень будет лежать левее точки 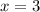 , а это будет означать, что к тому времени как функция подойдёт к
, а это будет означать, что к тому времени как функция подойдёт к 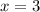 , она уже будет положительна (ведь правее экстремума
, она уже будет положительна (ведь правее экстремума 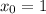 парабола рогами вверх будет идти только вверх). Исследуем:
парабола рогами вверх будет идти только вверх). Исследуем:
Победа.
ответ.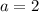 .
.
пусть ширина прямоугольника равна x см, тогда длина прямоугольника равна 4x см.
периметр прямоугольника вычисляется по формуле P = 2(a+b), где a и b - стороны прямоугольника. по условию задачи периметр прямоугольника равен 40 см. следовательно:
2(x+4x)=40
2*5x=40
10x=40
x=40/10
x=4 см
значит ширина прямоугольника равна 4 см, а длина прямоугольника равна 4x=4*4=16 см. прямоугольник со сторонами 4 см и 16 см имеет площадь, равную S=ab=4*16=64 см^2.
площадь квадрата вычисляется по формуле S=a^2, где a - сторона квадрата. из формулы площади квадрата можно вывести формулу для нахождения стороны квадрата. если S=a^2, то a=√S. следовательно, квадрат, площадь которого равна площади прямоугольника (то есть 64см^2), будет иметь сторону, равную
a=√64=8 см.
ответ: 8 см.