Итак,у меня есть 35 ,а у вас фото на котором нужно решить систему неравенств. за работу! первому написавшему лучший ответ : )

Показать ответ

Ответ:

MATEMATIK12345678

22.06.2020 19:53

$\left(\frac{(4-\pi)\sqrt2}{8-4\sqrt2};\ \frac{\frac\pi2-1}{8 - 4\sqrt2}\right)\!.$

Объяснение:

Область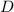 , задающая плоскую фигуру, координаты центра тяжести которого требуется найти, задана такими кривыми:

$y = \sin x;\\y = 0;\\x = \frac{\pi}{4}.$

Известны ограничения сверху и снизу на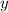 , а для только сверху. Тогда ограничение снизу будет граничным с остальными:

$\sin x = 0;\\x = \arcsin 0;\\x = 0.$

Получили четвёртое и последнее ограничение для области. Тогда область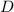 задана такими кривыми:

$y = \sin x;\\y = 0;\\x = \frac{\pi}{4};\\x = 0.$

Переведём условия в вид неравенств:

$D = \left \{ {{0\leq y \leq \sin x;} \atop {0 \leq x \leq \frac\pi 4.}} \right.$

Поскольку левые части неравенств области нулевые, можем сразу вычислить площадь области, не используя двойной интеграл, а вместо него использовав одномерный определённый интеграл, в качестве функции использовав верхний предел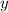 , а в качестве пределов интегрирования — части неравенства для .

$S_D = \int\limits_0^\frac\pi4\sin x \, \text{d}x = (-\cos x)|_0^\frac\pi4 = -\cos\frac\pi4 - (-\cos 0) = -\frac{\sqrt 2}2 + 1 = 1 - \frac{\sqrt 2}2.$

Как известно, если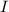 — точка центра тяжести, то 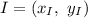$I = (x_I,\ y_I)$ , и они в свою очередь:

$x_I = \frac{\iint_D x\, \text{d}x\, \text{d}y}{S};\\y_I = \frac{\iint_D y\, \text{d}x\, \text{d}y}{S}.$

Найдём обе координаты точки центра тяжести.

Начнём с абсциссы:

$x_I = \frac{\iint_D x\, \text{d}x\, \text{d}y}{S} = (*).\\\\\iint_D x\, \text{d}x\, \text{d}y = \int\limits_0^\frac\pi4x\, \text{d}x \int\limits_0^{\sin x} \, \text{d}y \!:\\\int\limits_0^{\sin x} \, \text{d}y = (y)|_0^{\sin x} = \sin x.\\\int\limits_0^\frac\pi4 x \sin x \, \text{d}x = (**)\\\int x \sin x \, \text{d} x = -x\cos x + \int \cos x \, \text{d} x = \sin x - x \cos x + C.\\u = x;\ \ \ \ \text{d}v = \sin x \, \text{d}x\\\text{d}u = \text{d}x;\ v = \int \sin x \, \text{d} x = -\cos x + C.$

$(**) = (\sin x - x \cos x)|_0^\frac\pi4 = (\sin \frac\pi 4 - \frac\pi 4 \cos \frac\pi 4) - (\sin 0 - 0 \cos 0) =\\= \frac{\sqrt2}2 - \frac{\pi\sqrt{2}}{4\cdot 2} = \frac{4\sqrt2 - \pi \sqrt2}{8} = \frac{(4 - \pi)\sqrt2}{8}.\\\\(*) = \frac{\frac{(4 - \pi)\sqrt2}{8}}{1 - \frac{\sqrt2}2} = \frac{(4-\pi)\sqrt2}{8-4\sqrt2}.$

Теперь ордината:

$y_I = \frac{\iint_D y\, \text{d}x\, \text{d}y}{S} = (*).\\\\\iint_D y\, \text{d}x\, \text{d}y = \int\limits_0^\frac\pi4 \, \text{d}x \int\limits_0^{\sin x} y \, \text{d} y\!:\\\int\limits_0^{\sin x} y \, \text{d}y = (\frac{y^2}2)|_0^{\sin x} = \frac12 \sin^2 x.\\\int\limits_0^{\frac\pi4} \frac 12 \sin^2 x \, \text{d}x = (**)\\\int \frac12 \sin^2 x \, \text{d}x = \frac 14 \int 1 - \cos 2x \, \text{d}x = \frac14(\int \, \text{d}x - \int \cos 2x \, \text{d}x) = (***)$

$\int \cos 2x \, \text{d} x = \frac 12 \int \cos 2x \, \text{d}(2x) = \frac12 \sin 2x + C.\\\int \text{d}x = x + C.\\(***) = \frac14 (x - \frac 12 \sin 2x) + C.\\(**) = (\frac 14 (x - \frac 12 \sin 2x))|^\frac\pi4_0 = (\frac 14(\frac\pi4 - \frac12 \sin 2 \cdot \frac\pi4)) - (\frac 14 (0 - \frac12 \sin 2 \cdot 0)) =\\= \frac 14 (\frac\pi4 - \frac12 \sin \frac\pi2) = \frac 14 (\frac\pi 4 - \frac12) = \frac{\frac\pi2-1}{8}.$

$(*) = \frac{\frac{\frac\pi2-1}{8}}{1 - \frac{\sqrt2}2} = \frac{\frac\pi2-1}{8 - 4\sqrt2}.$

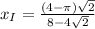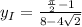ответом будут найденные координаты, $x_I = \frac{(4-\pi)\sqrt2}{8-4\sqrt2}$ и $y_I = \frac{\frac\pi2-1}{8 - 4\sqrt2}$ .

0,0(0 оценок)

Ответ:

link21

02.09.2021 19:02

В озере течения нет, значит по озеру катер S₁=20t₁ .

По реке катер шёл против течения, т.к. катер находился сначала в озере, а потом шёл вверх по реке. Значит S₂=(20-2)t₂=18t₂

Известно, что S₁=S₂, а так же что t₁+t₂>1.9, то есть

20t₁ = 18t₂ ⇒ 10t₁ = 9t₂

Если мы возьмём t₁ = 0.9, а t₂ = 1, то равенство сработает, но сумма будет равна 1,9 часа, что противоречит условию, так как известно, что катер шёл больше 1,9 часа. Значит нужно взять и умножить оба времени на 1,1 к примеру. Тогда получится:

t₁ = 0.9*1.1 = 0.99

t₂ = 1*1.1 = 1.1

S₁ = 20 * 0.99 = 19.8

S₂ = 18 * 1.1 = 19.8

S₁ = S₂ - условие удовлетворено

t₁+t₂ = 0.99 + 1.1 = 2.09 > 1.9 - условие удовлетворено

S₁ = S₂ = 19.8 км

S = 2*19.8 = 39.6 км

0,0(0 оценок)

Популярные вопросы: Алгебра